为什么圆的面积不是半径乘以周长？

半径绕圆心转一圈，扫过的确实是一个圆没错：

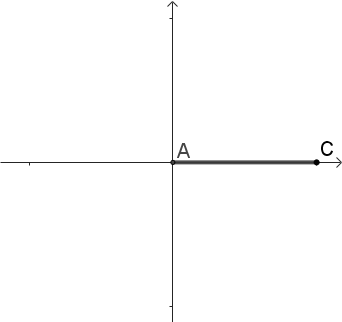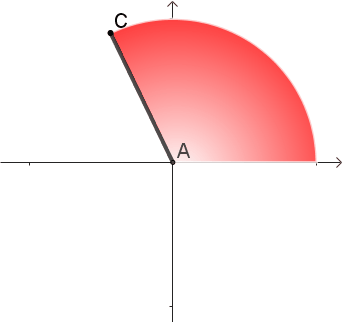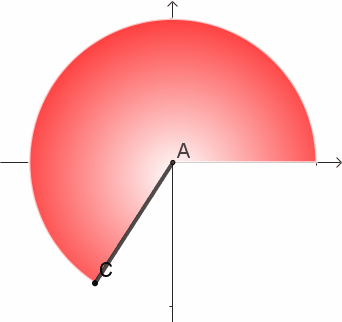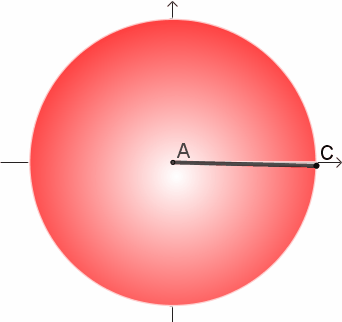
但是，观察上图会发现，和圆心的距离不同的地方扫过的“速度”也不一样。离圆心较远、红色的位置扫得快；靠近圆心的白色位置扫得慢。

圆的周长是最外侧C点走过的路程。问题的答案就在这里了，不能用跑得最快的C点代表整个半径。

A点：凭啥让我跟着你一起乘以整个周长？你在那儿转得开心，我压根就没动好吗？

半径上的每个点都乘以自己实际走过的路程，把这些路程加起来才是圆的面积。比如A点没动，那它的路程就是0；越靠外的点走过的路程也越长，直到C点走过的是整个圆的周长——最终这就变成了用积分的方式求圆面积。

我看到积分就头疼，不想弄得那么复杂……既然半径上的点都在运动，只是不同的点走过的路程有长有短。那么，是否有一个点，它走过的路程能代表半径上的所有点呢？

嘿，还真有！

半径是一根长度有限的直棍子对吧。要找这样一个点，让它站出来代表整根棍子上的所有点，凭直觉来说你觉得会是什么？

对，就是这根棍子的中点——它的重心，也就是下图中的D点。

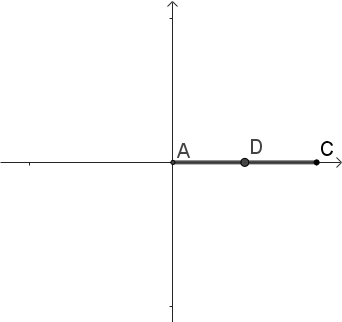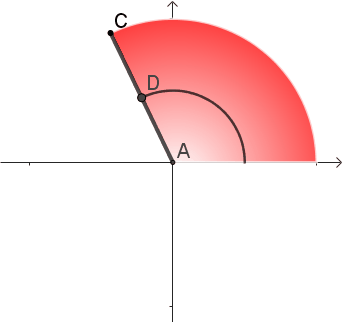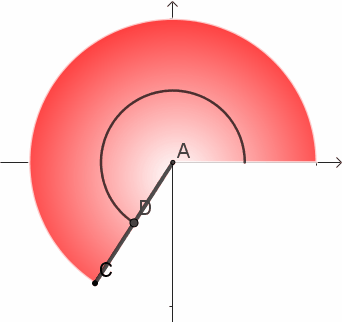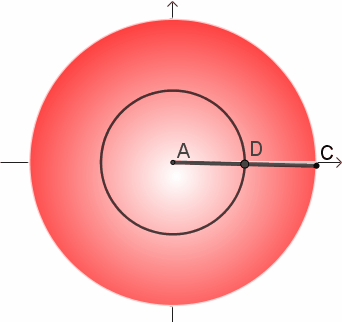
可以直观地看到，半径上位于DA之间的点，走过的路程比D点更短；位于DC之间的点，走过的应该更长。D点确实有能够代表整个半径的潜力~

是不是真的如此呢？简单计算一下：

设圆半径为 ，那么D点的路程是半径为 的圆周，周长是

它与原始半径的乘积则是 ，是圆的面积没错。

不会是巧合吧，这种方法通用吗？

当然。再看个三维空间的例子，回想一下小学就学过的圆锥体积公式 ，它是同底同高的圆柱体体积的三分之一。

圆锥可以看作一个直角三角形绕某条直角边旋转一圈得到。这个三角形的重心与旋转轴的距离，正好是另一条直角边的三分之一。

这两个“三分之一”冥冥之中是有关联的：

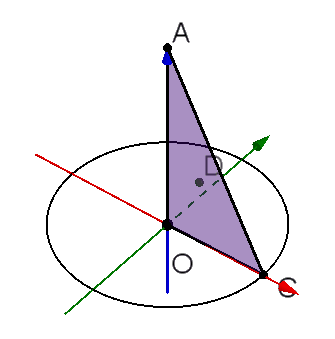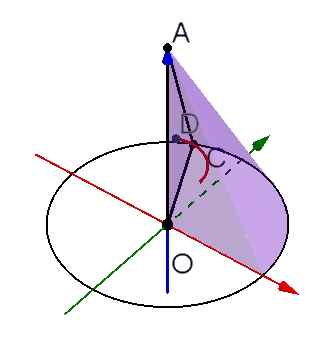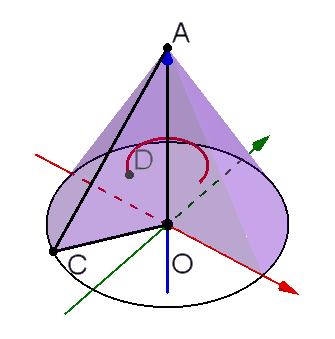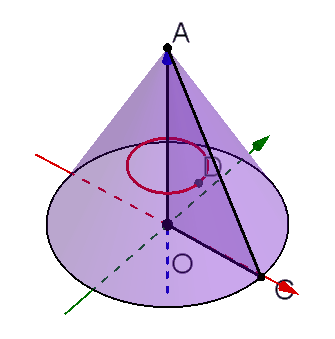
图中的AOC是旋转形成圆锥的三角形，其中 ， 。D是重心，那么D至AO的距离就是它的旋转半径 。D在旋转时走过的路程，也就是红色小圆的周长是

AOC的面积是 ，两者相乘正好得到 ，就是圆锥的体积了。

这个规律是符合直觉的。一个图形的重心在某种程度上代表了整个图形，图形在旋转时每一点走过的路程各不相同，但重心走过的路程是最有代表性的。

实际上这就是帕普斯质心定理（Pappus's centroid theorem^[1]，也叫帕普斯-古尔丁定理），由古希腊数学家亚历山大的帕普斯（Pappus of Alexandria^[2]）提出，后又由瑞士数学家保罗·古尔丁（Paul Guldin^[3]）整理并证明。它的原始版本分成两部分：

帕普斯第一定理：一条曲线绕此曲线以外的某一个旋转轴形成旋转曲面，其面积等于「曲线的长度」乘以「曲线的重心在旋转时走过的路程」。
帕普斯第二定理：一个曲面绕此曲面以外的某一个旋转轴形成旋转体，其体积等于「曲面的面积」乘以「曲面的重心在旋转时走过的路程」。

现在看甜甜圈（环面）的表面积和内部体积公式是不是就很显然啦。小圆是生成元，大圆是小圆重心（圆心C）的轨迹，甜甜圈的表面积就是小圆周长乘以大圆周长，体积则是小圆面积乘以大圆周长。

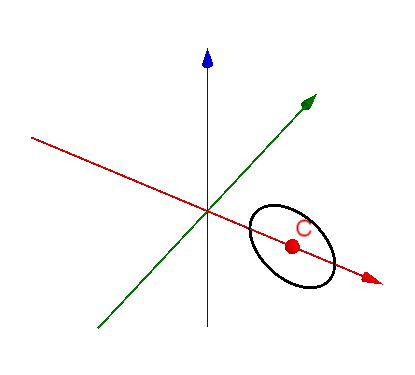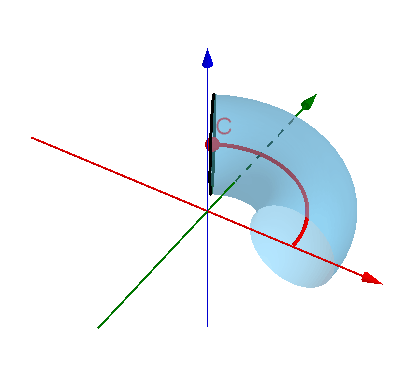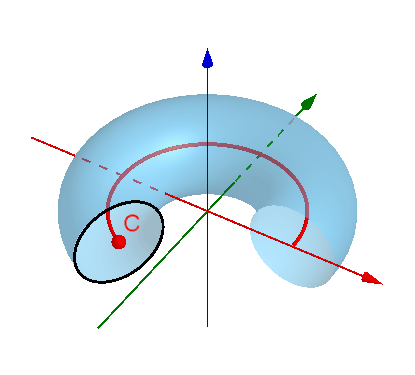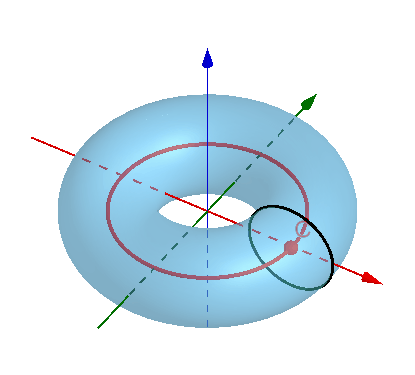
要是环面是一个有棱有角的方形产生的，阁下又该如何应对？

比如一个倾斜45°边长为1的正方形，绕半径为2的圈旋转产生的“咯手甜甜圈”

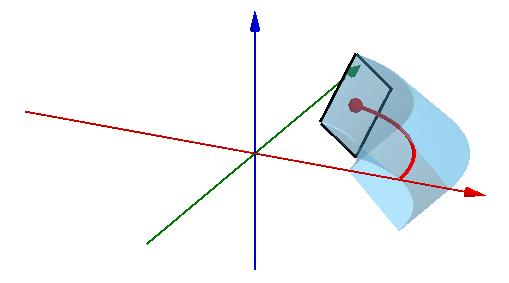
用传统的积分方法来算就比较麻烦了，而根据帕普斯定理，能很快得知它的表面积是 ，体积是

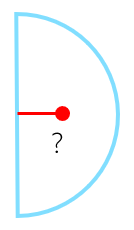
反过来说，这个定理也可以用来找一些图形的重心。比如圆的重心是圆心，那半圆（面）呢？它的重心会偏离圆心多少？

让半圆沿着自己的直径旋转一周得到球体：

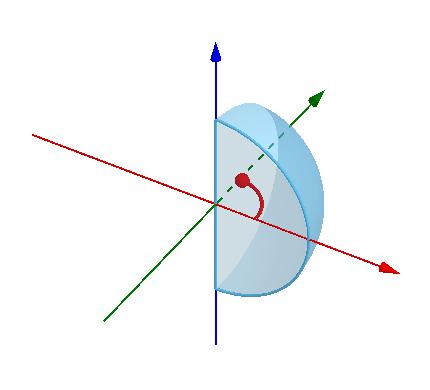
球体体积是 ，半圆的面积是 。根据帕普斯第二定理，半圆的重心轨迹周长是

那么轨迹的半径，也就是重心与半圆圆心的距离是 ，比半圆半径的一半略小一点：

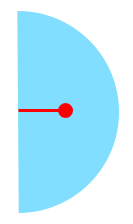
类似地，半圆周旋转一圈得到球壳面积为 ，半圆周长度则是 ，用帕普斯第一定理可以得知半圆周的重心在离圆心 处：

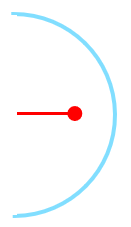
练习题：要是半圆周加上直径，它的重心离圆心有多远？

注意这个时候不能让它绕着直径旋转了，旋转轴要稍微离远一点:

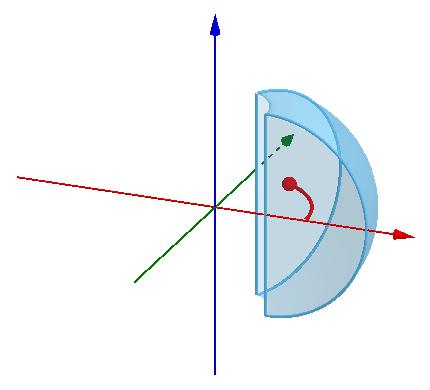
这是帕普斯定理应用时需要注意的：生成元是二维的，比如半圆片时，将它贴在旋转轴上不会有影响；生成元是一维的，比如这里的半圆周+直径，那么旋转轴就不能再与直径重合。否则，直径不会因旋转产生表面积，却会对重心有影响。

结果是 ，当然它也可以用半圆周和直径加权平均得到。

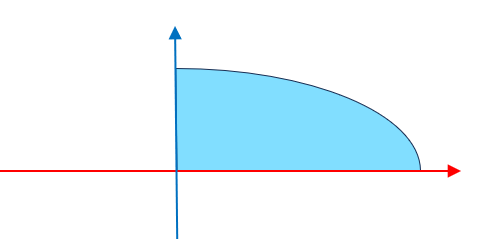
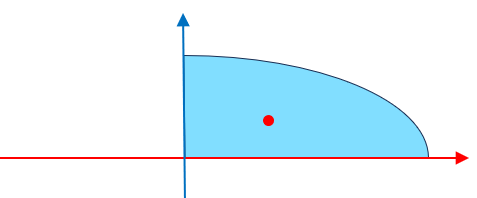
再看最后一个例子，一个四分之一椭圆片，放在xz平面中的话它是 的一部分，面积是 。它的重心在哪儿呢？

让它绕z轴转一圈，得到半椭球

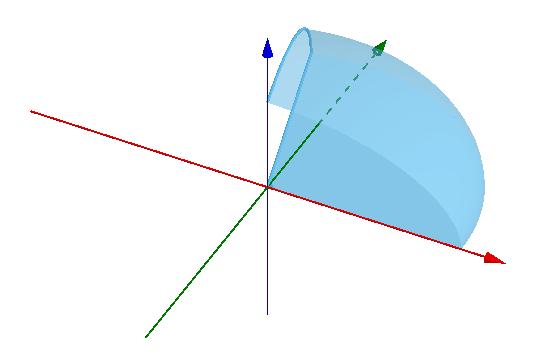
其体积是 ，那么重心的x坐标是

由于椭圆片不是关于xy平面对称的，重心的z坐标也未知。为了找到它，可以再让椭圆片绕x轴转一圈，得到第二个半椭球

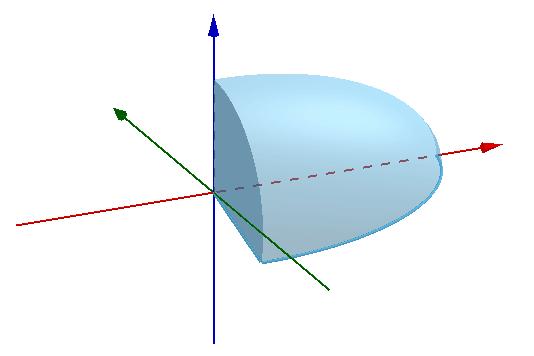
体积 ，重心的z坐标是

所以这个椭圆片的重心在 ，大概这个位置：

如果要在复杂的形状上应用帕普斯定理，需要注意几点：

• 旋转轴不能与生成元的任一部分重叠（在生成元自身的维度上，它与旋转轴相交的部分测度必须为0）

比如，以原点为中心的一条斜线段作为生成元，绕z轴旋转。生成元与z轴相交的部分是原点本身，这个点在生成元的维度（1维）上测度为0，没有重叠：

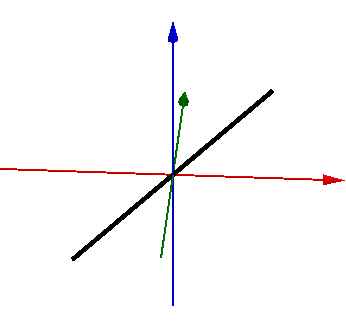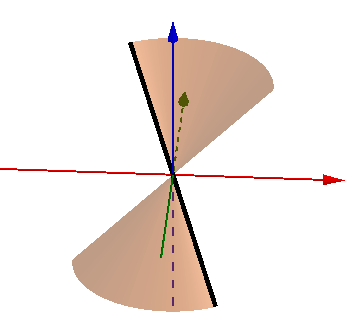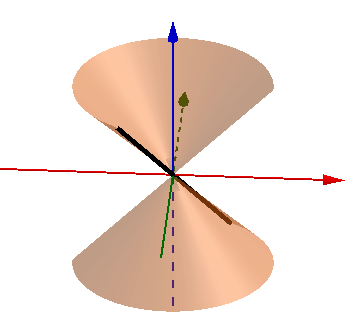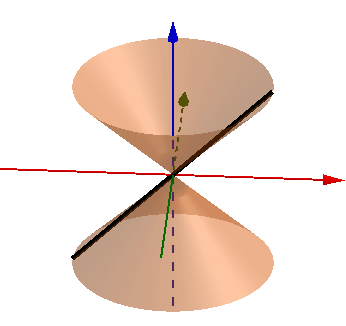
前面举的半圆周+直径例子则需要注意：生成元是1维的，那么旋转轴与生成元相交的部分就不能在1维上可测，因此不能选择直径本身作为旋转轴。

• 旋转轴不一定要远离生成元。只是当旋转轴穿过生成元，将它分成两块或更多时，每一块都需要单独考虑。

这一点与物理中求物体的转动惯量的方法类似。还以上图为例，线段绕z轴旋转会产生一个锥面。但这时候显然不能用整个线段的重心（原点）来计算，需要分别处理原点分割的两部分线段。

• 生成元需要时刻与重心的轨迹垂直。并且在旋转过程中，新生成的不能与已经生成的部分重叠。它们可以互相穿过，但相交的部分在最终旋转体的维度上测度必须为0。

例如两根长度相同的线段分别水平和竖直放置。旋转后圆环和圆柱面会相交，但相交的部分是一条曲线（圆周），这在最终需要衡量的维度（二维曲面）上的测度（面积）为0：

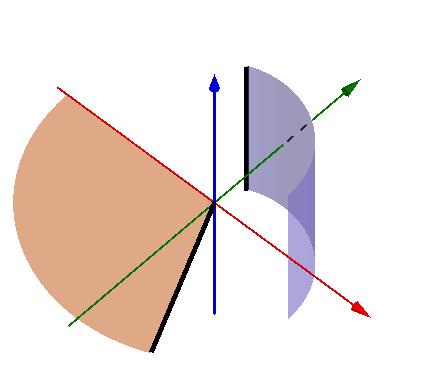
这种情况就可以直接用帕普斯定理。当然，两个曲面的面积仍需分开计算。

再看平面上的一个反例。一条横着的棍子绕原点旋转，会产生一个圆环对吧：

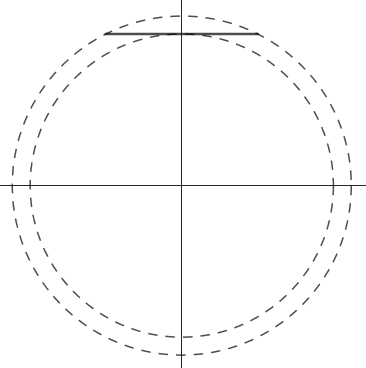
但是这根棍子的左右两半部分划过的面积会互相重叠。蓝色是棍子左半部分产生的面积，紫色是右半部分，两者会在红色部分打架：

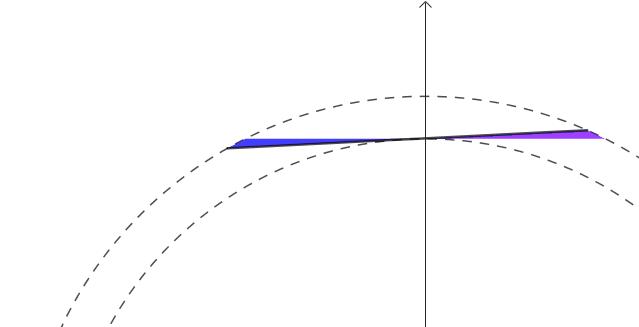
最终的旋转体是二维的圆环，而重叠的区域也是二维的，因此不能直接对整个棍子用帕普斯定理。棍子转过完整的一周，圆环实际上被重复生成了两次。计算时只保留左半或者右半根棍子才能得到正确结果。

另外，这个小棍与旋转的方向不垂直，不能用小棍的长度作为生成元的测度进行计算，需要把它投影到与重心轨迹始终垂直的直线上。

• 旋转不必转完整个圆周，也可以只转过一定的角度，此时用重心走过的圆弧长度作为乘数即可。

这一点容易理解，旋转产生的几何体有着一定的旋转对称性，像切蛋糕一样切出它的一个“角”，占总体积的比例等于此角与整个圆周的比例。

以现代数学的眼光看，这个定理完全可以推广到更到的维度，不必局限于三维空间中的旋转面或者旋转体。如果一个p+q维流形A，可以由一个p维流形B绕一条q维的轴旋转得到，那么A的p+q维测度就是「B的p维测度」乘以「B的重心旋转时产生的q维测度」之积。