高等数学在工程领域中有哪些实际应用？

高等数学主要部分就是微积分，以及求解微分方程。高等数学在工程领域中的运用比比皆是，多得不甚枚举，打开任何一本工程理论类书籍都能看到。

以下，我们来看电气工程中的几个例子吧。

1.线路开断过程中电流相对时间的导数dI/dt意义之解析

早些年供电不是很稳定，常常停电。每次停电前瞬间，灯光会特别亮一下，然后就停电熄灭了。

对于这种现象，老师的解释是：电流和水一样。突然把水闸关闭，水流的冲击力会使得水闸前的水位瞬间升高，所以停电前电压会瞬间上升。老师说，正是这种电压瞬间上升造成灯光闪亮一下再熄灭。

现在我们都知道了，这其实就是开断感性电路时产生的过电压。

我们看下图：

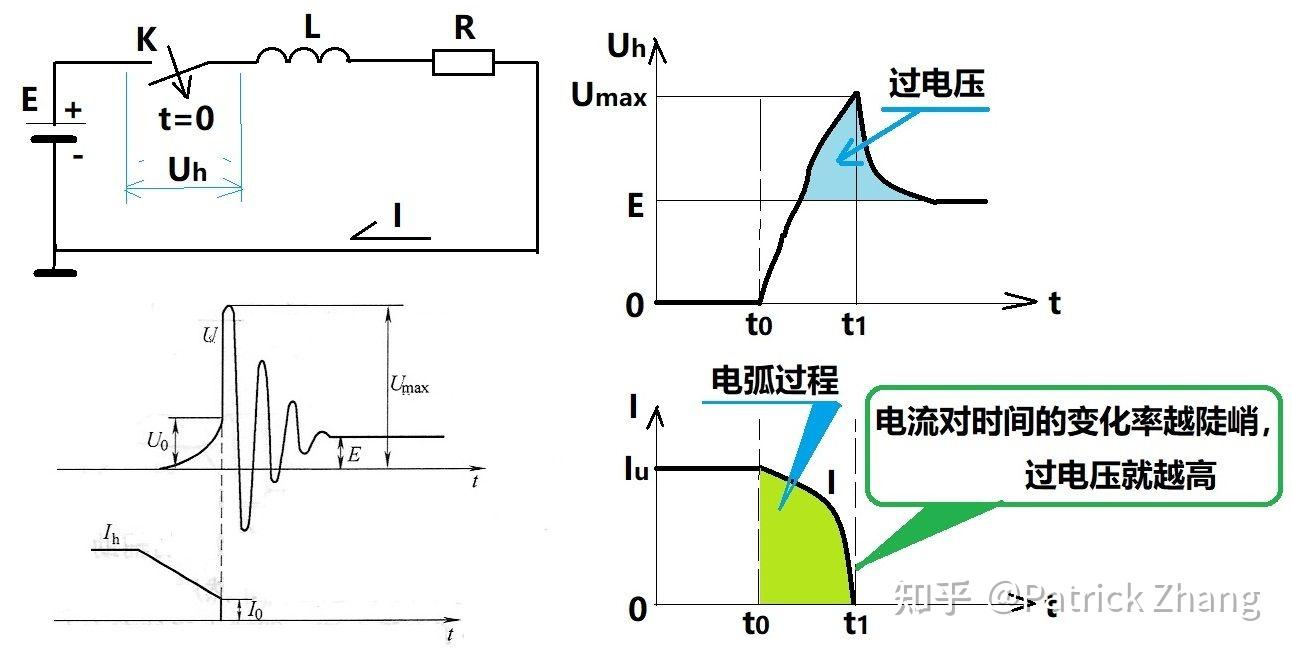
我们看图2左上侧的电路图，当开关K开断的起始时刻t0，触头间电压等于零。随着电流减小动、静触头开距增大，电压持续升高。当电压超过击穿电压后极间气体产生电弧，我们设电弧电压是Uh，其电路方程如下：

，式1

我们看到，电感产生的反向电动势LdI/dt与电源电动势E叠加在一起加载在开关K的两极之间，可见过电压还是很强烈的。

电流I随着时间的推移其值越来越小直至等于零，开关K动、静触头间的电压稳定保持在电源电动势E。

注意看电流I相对时间t的变化率dI/dt， 也即电流对时间的导数。我们发现电流减小得越快，dI/dt的绝对值就越大，开关K的开断过电压就越高。另外，我们要注意到过电压并不仅出现在开关K的动、静触头上，其实过电压加载在电源上，因此会对线路中所有电器都带来威胁。我小时候看到的停电前的灯亮闪，其实就是过电压的反映。

我们看到，过电压与导数和微分挂上了钩，这也算高等数学的运用之一吧。

另外，图2左下图我们看到了振荡波，它是电感与分布电容产生的衰减性振荡。此振荡波的分析涉及到求解微分方程。由于过程繁复，这里就不介绍了。

我们看下图：

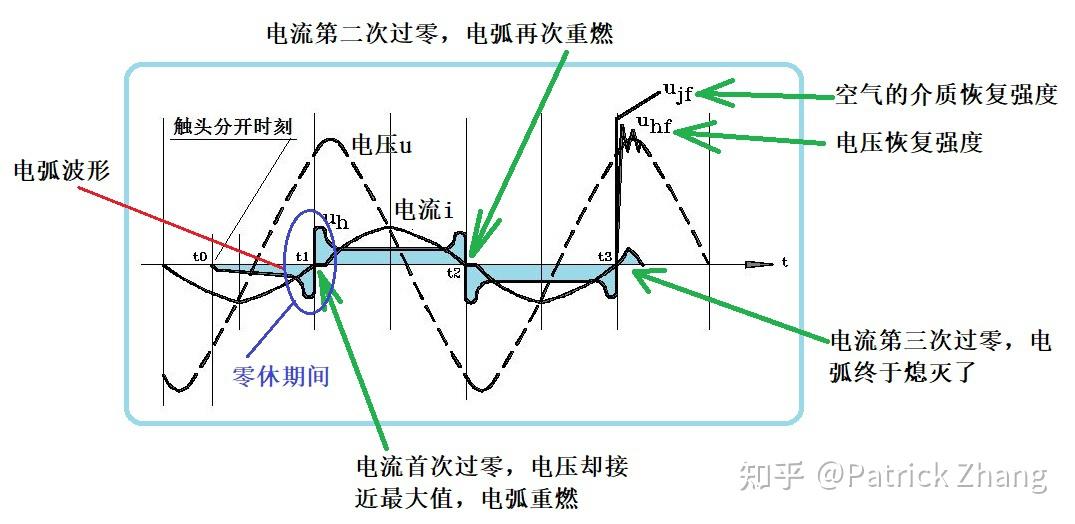
图3是交流电弧的电压和电流波形。我们在t3时刻看到电弧熄灭时的电压波形，并看到电压波形上有寄生振荡，此震荡波就是感性负载的电感量与分布电容振荡的结果。

2.直流磁路漏磁系数法分析中出现的积分关系

我关于直流磁路的教学课件摘录如下：

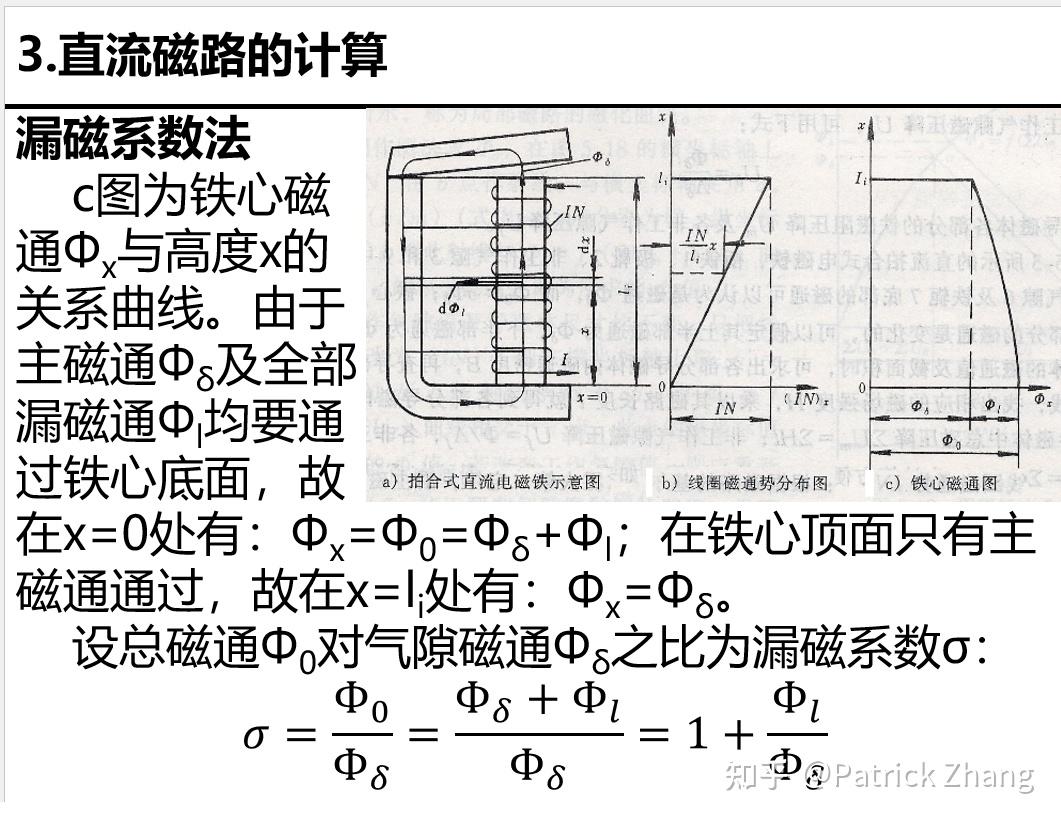
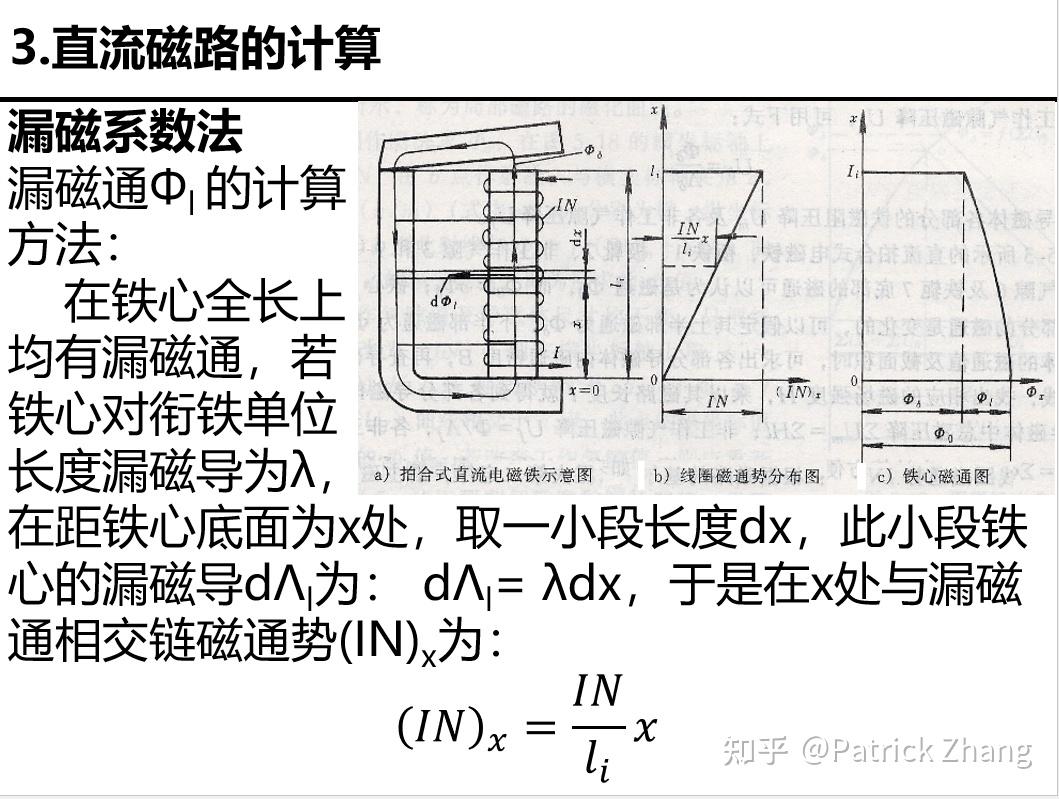
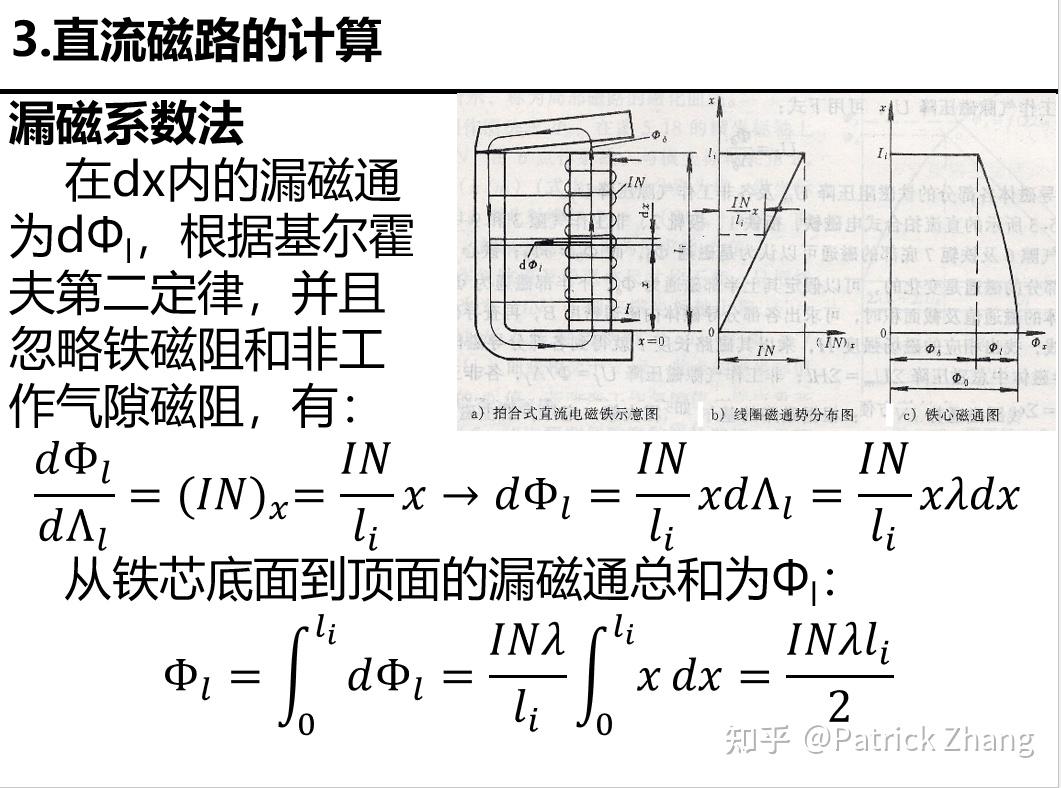
我们看到，当我们用漏磁系数法推导漏磁通 时，用到了简单的定积分，由此得到结果：

，式2

此法在分析继电器磁路系统时得到广泛运用。

3.结论

其实，在电气领域中应用的不止是高等数学，线性代数和复变函数也应用十分广泛。特别是自动控制，几乎都是复变函数。

为何如此？因为在高等数学中求解微分方程太麻烦，把方程用拉普拉斯法变换到复数域中，微分方程就成为代数方程，求解容易。得到结果后再反变换回来，进一步求解就能得到结果，方便快捷。此外，用复数把电参量变成相量，以此求解交流电路，也会方便很多。

高等数学在工程领域的应用非常广泛，值得仔细研究。