如何从概率的角度计算三国杀国战模式的胜率?

先说结论：在绝对理想^[1]的情况下，这个概率是 30.47%。

对整个胜率的计算，分为两个部分：

1. 某种势力分布发生的概率；
2. 在这种势力分布下，所有人的平均胜率；

下面我们以某一种情况为例，来说明整个概率的计算过程。

8 个人，其中 5 个人为第一个势力，2 个人为第二个势力，1 个人为第三个势力。

一、该势力分布发生的概率

根据「古典概率」：一个事件发生的概率 = 这个事件的不同组合数 / 所有事件的不同组合数。

不失一般性，不妨设 A 势力 5 个人，B 势力 2 个人，C 势力 1 个人。

考虑 A 势力，由于有 15 个武将可以选择，选出 5 组不同武将的组合数有多少呢？

• 先选出第 1 个武将，组合数为 ；
• 然后依次选出第 2 ~5 个武将，组合数为 ；
• 这 5 个武将有 5! 种排列；

组合数

类似地，我们得出，对于有 n 个武将的势力，组合数：

又由于，A、B、C 三个势力人数不同，可以互换，所以总共的组合数：

而所有情况的总组合数，可在之后枚举完后加和。

二、该势力分布发生时，所有人的平均胜率

由于该分布发生时，最后一个第一个势力的玩家将成为「野心家」，因此势力分布变成了 4+2+1+1；

本问题有一个强假设（实际上很难成立）：所有人的获胜概率相等；

那么拿到第一势力的前 4 个人，胜率就是 1/2；第二势力 2 个人，胜率为 1/4，第三势力和野心家的胜率为 1/8；

综合来看，胜率为： ，也就是 34.375%

以上是其中一种势力分布的计算情况。

事实上，不同的势力分布情况共有 14 种，其中 6 种会出现「野心家」（即一个势力不少于 5 人），剩下的情况有 8 种。如果所有势力不等价，则有 161 种情况。如下表所示：

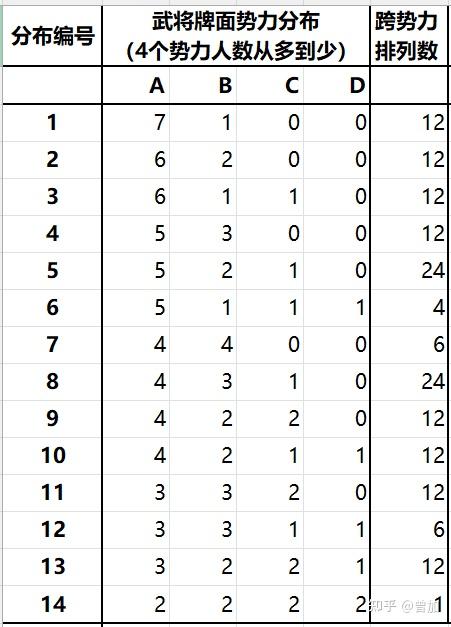
无需编程，用 Excel 即可处理数据，我们有下表：

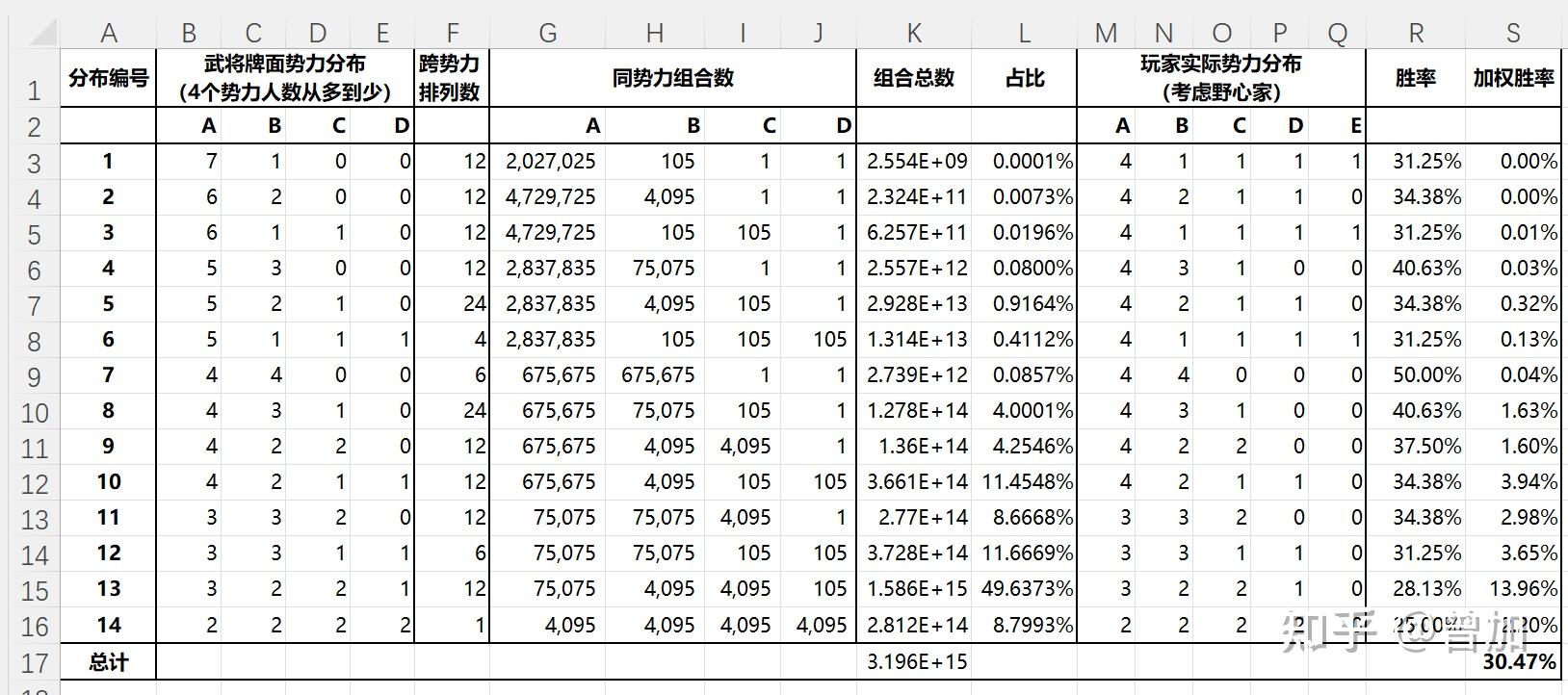
其中：

同势力组合数：G3=PERMUT(15,B3*2)/2^B3/FACT(B3)
组合总数：K3=PRODUCT(F3:J3)
胜率：R3=1/64*SUMSQ(M3:Q3)

最终我们得到：总体的胜率为 30.47%；

不过，在实操层面上，概率会有些不同；一方面，部分势力会有更高的登场率；另一方面，拥有 4 个武将的势力（这种情况发生的概率名义上是 21.2%，实际上会更高）较容易拥有优势，胜率往往会超过 50%，以上情况都会使得总体胜率略微高于这个数。

最后：我觉得这个问题还经典的，它好就好在，其背后的数学原理，从知识层面上讲不会超过高中数学（主要就是「排列组合」和「古典概率」），如果学奥数的话，可能小学高年级就学过了。但若要真要把这个问题算准确，那对这两个分支的理解也算是比较深刻了。而在实操过程中，用 Excel 可以对结果进行准确计算，然后顺便把 Excel 的很多函数也整明白了。