请问有没有人简单解释一下光学系统中球差和像差的区别?
0. 前言
这是一个系列专栏,主要讲光学像差理论,我目前的计划是先讲 5 种初级像差,后续可能会讲像差平衡以及其他内容。
主要参考书有 2 本:
《Optical Imaging and Aberration. Part I》
《Introduction to Aberrations in Optical Imaging Systems》
还有一本小册子有时也会用到:《Field Guide to Geometrical Optics》
在阅读本专栏之前,建议先看我哥的专栏文章,以此对波像差 Wave Aberration 和光线像差 Ray Aberration 有大致了解。
YanSR:【1】像差理论:波像差 Wave AberrationYanSR:【2】像差理论:光线像差 Ray Aberration在知乎写这种干货文章其实是件很花时间的事情,文章里的图片也基本是我自己画的,我个人觉得我写得还算用心。
创作不易,如果你觉得这篇文章对你有所帮助,请点赞、关注支持一下,只收藏不点赞的话,我会伤心的哟 o(TωT)o
1. 球差
球差的波像差 Wave Aberration 表达式为
这里对
做了归一化处理,即
光线像差 Ray Aberration 的表达式为 这里
代表 F-number。注意
,因此在用
表示
时要加一个负号。
( 与
的关系推导,以及
的相关内容,详见我哥的文章)
对于球差,其光线像差为(对于凸透镜,通常有
,这里及下文均以凸透镜为例来讨论)
从上述表达式中,可见球差的 Ray Aberration 只与 Aperture Vector 有关,与 Field Vector
无关,且
的方向与
相同,大小随
单调递增。球差的示意图如图 1 所示。
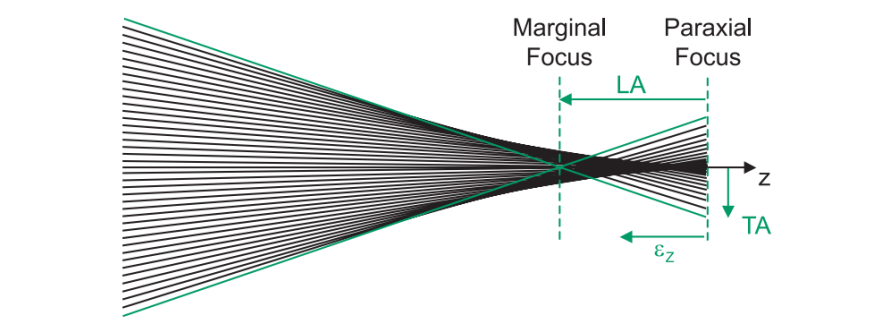
2. 球差+离焦
当球差和离焦 Defocus 同时存在时,波像差 Wave Aberration 为 光线像差 Ray Aberration 为
由于
,为了减小
(用离焦来平衡球差),需要使
离焦系数 与实际离焦量
成正比,两者的关系为
证明过程可以看我哥的笔记(如果他愿意写的话)
这里 是有符号的,
和
表示将像面朝出瞳移动。离焦系数
与实际离焦量
的关系如图 2 所示。
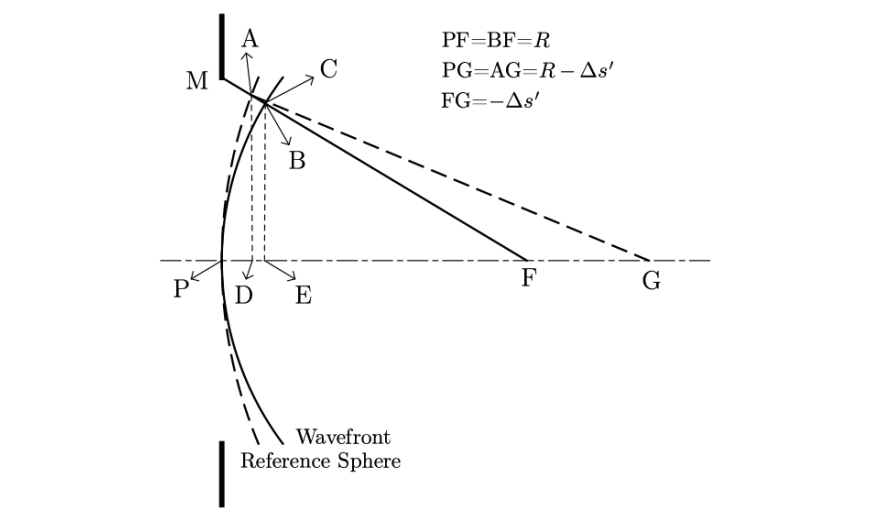
令
,解得
或
(
)
记 ,
,
随
和
的变化如图 3 所示(图中将
做了归一化处理)
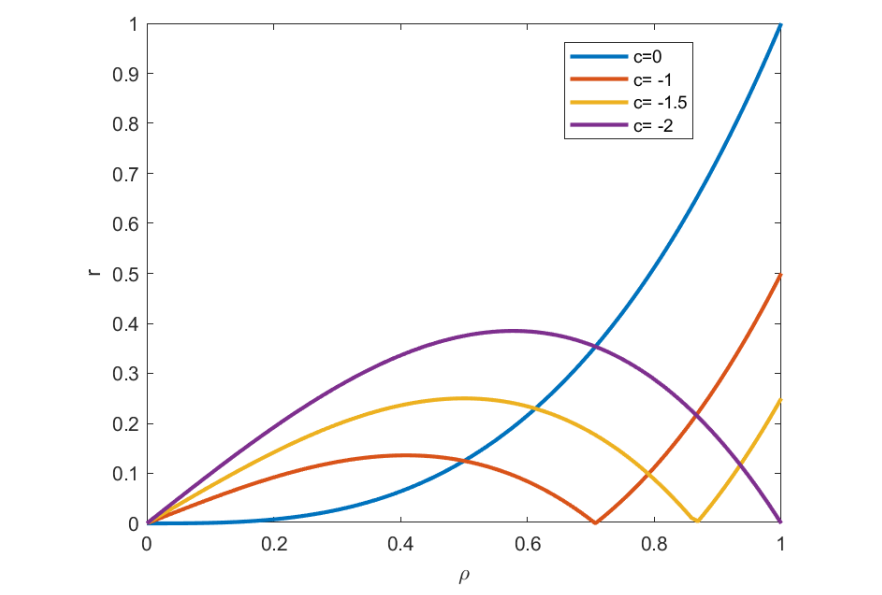
从图 3 可以看出,当 时,
的最大值要么在顶部的拐点处(
), 要么在
处。
将
做归一化处理后,有
令
,解得
,对应的
为
时,对应的
为
2.1 Marginal Focus
下面来探讨当离焦系数 (或
)取何值时,边缘光线的 Ray Aberration
,这实际上也是在确定边缘光线的焦点位置(Marginal Focus)
由于 表示边缘光线(
)的 Ray Aberration 的半径,当我们想要用离焦来平衡边缘光线的球差时,令
,解得
,这与图 3 的结果一致。
小结1:当 ,即
,实际离焦量
时,边缘光线的球差得到平衡,
其实就是边缘光线的焦点(Marginal Focus)到高斯像面的距离,即纵向球差 Longitudinal Aberration.
2.2 Min Circle
下面来探讨当离焦系数 (或
)取何值时,像面处的几何光斑半径最小(Min Circle)
几何光斑半径指的是可以包围住像面弥散斑的最小圆圈的半径,注意与RMS 光斑半径区分。
设像面处的几何光斑半径为 ,显然
为
的最大值,因此
也是
和
中较大的那一个,即
,
和
随
的变化关系如图 4 所示
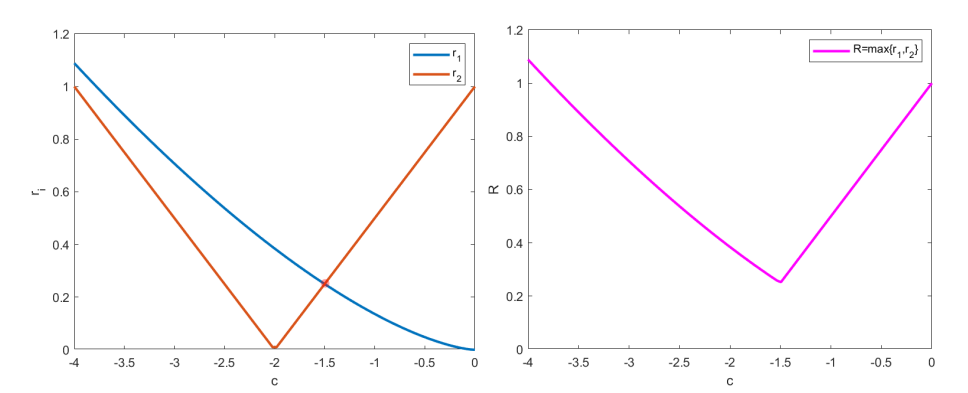
从图 4 可以看出,当 时,
取最小值。
令 ,解得
(舍去) 或- 1.5
当 时,
取最小值,此时
,对应
和
当 ,即像面不发生离焦,像面为高斯面时,
,对应
小结2:当 ,即
,实际离焦量
时,像面处的几何光斑半径最小,此时的几何光斑半径是高斯像面(无离焦)的
倍。与小结1对比可知,离焦量
是
的
倍
2.3 Min RMS
下面来探讨当离焦系数 (或
)取何值时,像面处的 RMS 光斑半径最小(Min RMS)
RMS 光斑半径即 Root Mean Square Radius,注意与上一小节中的几何光斑半径(Min Circle)区分。
Ray Aberration 的表达式如下:
由于
与
的方向相同,且关于光轴对称,所以像面弥散斑的质心一定落在高斯像点处,RMS光斑半径实际上也是像面弥散斑坐标(以高斯像点为原点)的标准差
仍记 ,
的表达式如下:
证明过程详见参考书《Optical Imaging and Aberration. Part I》4.3.1节
随
的变化关系如图 5 所示(图中已将
做归一化处理)
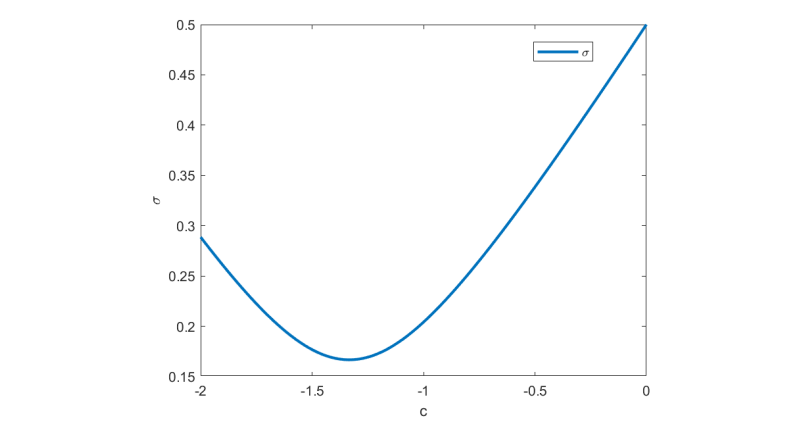
为了求出 为何值时,
取最小值,令
,解得
,此时
当 ,即像面不发生离焦,像面为高斯面时,
小结3:当 ,即
,实际离焦量
时,像面处的
RMS光斑半径最小,此时的几何、RMS光斑半径是高斯像面(无离焦)的 倍。与小结1对比可知,离焦量
是
的
倍
注:Min RMS像面位置的另一种证明方法,见参考书《Introduction to Aberrations in Optical Imaging Systems》 8.6.1节
2.4 Mid Focus (Min Wavefront Variance)
Mid Focus 指的是处在高斯像面和 Marginal Focus 中间的像面,此时的离焦量是 Marginal Focus 的一半,即
Mid Focus 的几何光斑半径 是高斯像面的一半,即
Mid Focus 有一个特殊的性质:它有着最小的波前方差(Min Wavefront Variance)
下面来证明这一性质:
波像差的方差为 其中
波像差
代入上式有
于是
显然,当
时,波前方差
取最小值
注意:这里的 指的是波前方差,它是对波像差
进行计算,而 2.3小节 Min RMS 中的
是对光线像差 Ray Aberration
进行计算。
小结4:当 ,即
,实际离焦量
时,像面处的波前方差最小,此时的几何光斑半径是高斯像面(无离焦)的
倍。与小结1对比可知,离焦量
是
的
倍
3. 总结
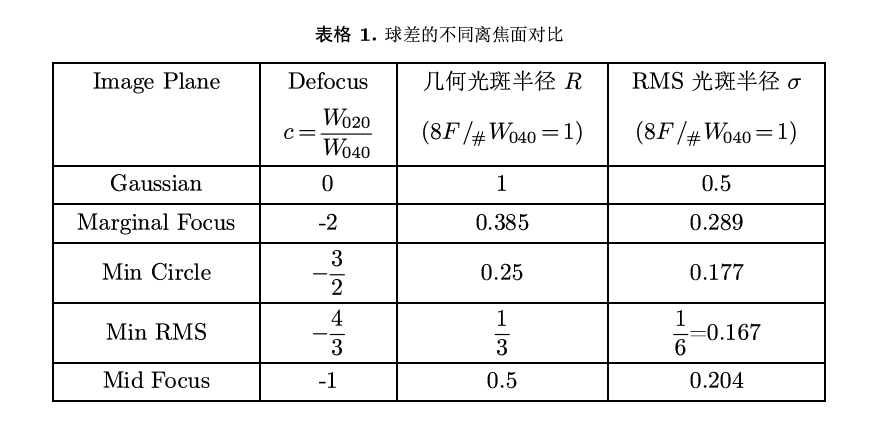
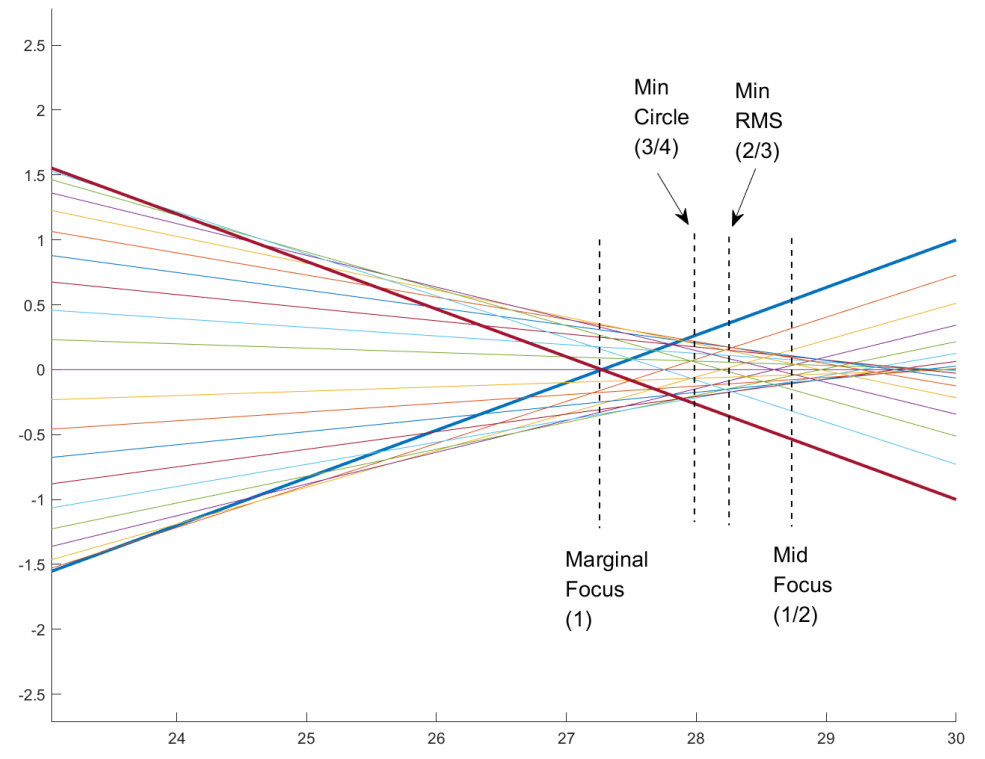
在知乎写这种干货文章其实是件很花时间的事情,文章里的图片也基本是我自己画的,我个人觉得我写得还算用心。
创作不易,如果你觉得这篇文章对你有所帮助,请点赞、关注支持一下,只收藏不点赞的话,我会伤心的哟 o(TωT)o