有哪些不易察觉的错误证明？

四色定理的错误证明曾经在全世界数学家眼皮底下瞒天过海11年。

英国数学家Kempe在1879年发表了他的的四色猜想“证明”，此证明短小精悍，思路奇巧，被数学家群体广泛认可，四色猜想从此被称为四色定理。直到1890年P. J. Heawood发现证明中看似微小的漏洞。当时的人们不会想到，这小小的漏洞成为了怎么打补丁也打不完整的破口，一次次的错误尝试背后揭露了越来越复杂的本质。一直要等到物是人非，将近一个世纪以后的1976年，才被人们用计算机暴力穷举，跑完了四色定理证明接力赛的最后一棒。

这篇回答里我们来零距离欣赏一下Kempe那瞒天过海的奇妙“证明”。答主用了一套新的方式来命名一些概念，以求使过程更清晰易读。但是其中贯穿的思路，绝对忠于Kempe原文。

四色定理表述

在一张包含有限个国家的平面地图上，如果每一个国家都占据一块连续的区域，那么只需要用四种颜色给每个国家上色，就可以使所有的邻国具有不同的颜色。

所谓连续区域，是指其中任何两点都能找到一条宽度始终大于0的路径连通。所以允许存在环形国家。但是只交于一点的两块连续区域并不互相连通。

所谓邻国是指拥有邻边的国家。只有邻点的不算为邻国，所以允许颜色相同。

（我们不讨论如何用拓扑学或者图论语言严格表述四色定理，因为要理解四色定理的实质并看懂Kempe的证明，这样直观的定义已经足够了）

证明需要用到的定义

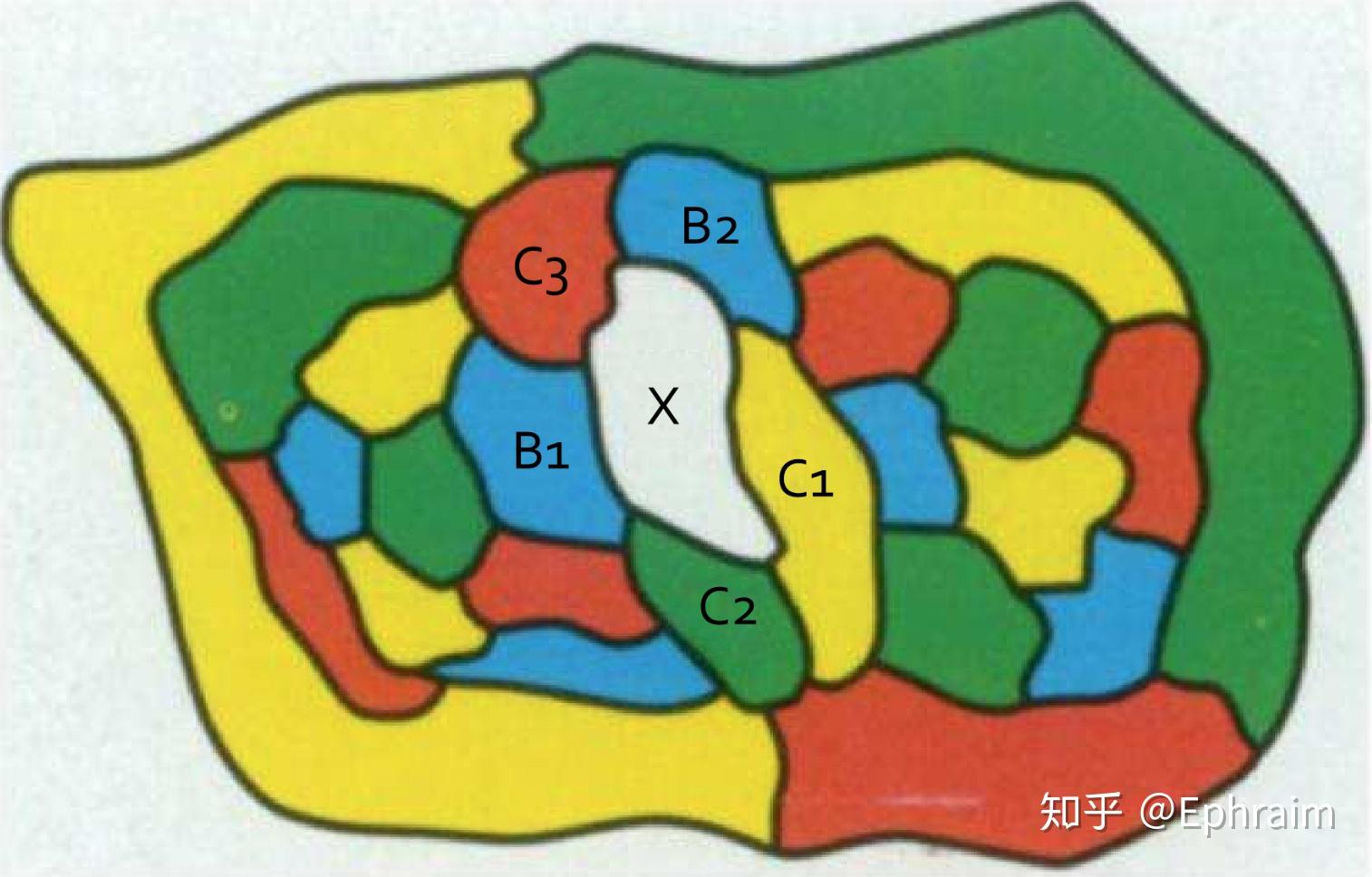
定义1 一个“联盟”指的是地图上只由两种颜色构成的、不能再延伸（这一点必不可少，感谢评论区指出）的连续区域。很显然，两种颜色将会在这个联盟中交替出现。如下面左图黑粗线内部区域，是一个“蓝绿联盟”。

注意到，根据另一个颜色的选择，一个国家同时属于最多3个不同的联盟。

定义2 我们称两个国家 与 “同盟”，如果它们拥有一个共同的联盟。反之，称 与 “不同盟”。

注意到两个邻国必然同盟。如果 与 不同色，说它们同盟，等价于说 所在的拥有 的颜色的联盟包含 。如果 与 同色，说它们同盟，等价于说 所在的3个联盟中至少有一个包含 。

定义3 我们可以对联盟进行一种操作，称做“反相”，使得内部两种颜色互换。下面右图是反相后的结果。

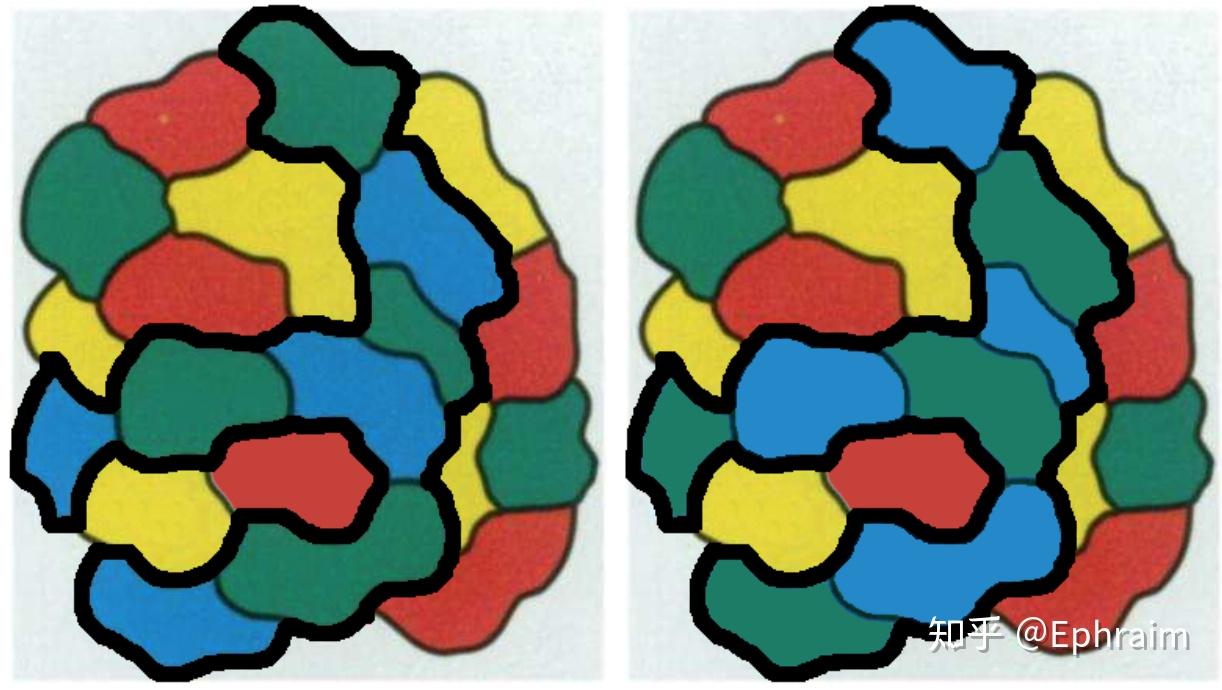
引理1 如果一个地图的所有邻国不同色，那么反相任何一个联盟之后，所有邻国依然不同色。

证：显然。

引理2 对于任何一张包含有限个国家的地图，至少存在一个国家的邻国数量不超过5。

证：使用反证法假设所有国家的邻国数量都不少于6。由欧拉定理可知 。
一方面，任何一个交点 至少与3条边相连，考虑所有交点的邻边数量总和

另一方面，任何一个国家 至少有6个邻国，考虑所有国家的邻国总和

代入欧拉公式得到

矛盾。所以至少存在一个国家邻国数量不超过5。

定义4 我们用“三国交点”表示三个国家邻边的交汇。等价的说法是，“三国交点”定义为连接正好3条边的顶点。

开始证明

使用归纳法。对于只有 个国家的地图，四色定理显然成立。现在需要证明当四色定理对 个国家的地图成立时，四色定理对 个国家的地图依然成立。

对于一个有 个国家的地图 ，根据引理2，我们总可以找到某一个国家 具有不超过5个邻国。考虑地图 刨去 之外的部分，记为 ，这是一个有 个国家的地图。现在四色定理对于 成立，所以 可以用四种颜色填充使任何邻国不同色。

现在假设已经完成 的四色填充，而 仍然是黑色。我们考虑怎样使用反相等操作对其进行调整，最后可以给 填充四种颜色中的一种，完成地图 的四色填充。

情形1 若 的邻国数量不多于3。那么把剩下一种颜色给 ，即可完成的四色填充。

情形2 若 具有4或5个邻国，但所有邻国只有不多于3种颜色。同样把剩下一种颜色给 ，即可完成 的四色填充。

情形3 若 有4个邻国，分别具有不同的颜色。将四个邻国分别记为 。

首先注意到，一定可以找到其中某两个邻国 与 ，使得 的三国交点不存在。

证：假设对任意都存在一个三国交点，记为 。那么由于 三个三国交点的存在，而一条邻边只有两个端点，可以断言 与 至少有两条邻边。这意味着 构成一个环形结构，将 划分成互不连通却都与 相邻的至少两个区域。由于 只有4个邻国，除去 还剩3个，在 中必然有一个属于其中一个区域，另外两个属于另一个区域。由于两个区域不连通，这些三国交点不可能同时存在，矛盾。

将这两个邻国记为 与 ，现在我们可以将情形3细分。

情形3.1 若 与 不同盟。那么将 所在的带有 颜色的联盟反相之后，将会具有和 相同的颜色。此时将剩下一种颜色给 ，即可完成 的四色填充。

情形3.2 若 与 同盟。

我们注意到，此时 与 必不同盟，且 的三国交点必不存在。

证：将 与 的共同联盟记为 ，那么 必然构成一个环形结构。因此 至少包含两块互不连通，却分别与 相邻的区域。而 只有4个邻国，因此 与 分属于这两块互不连通的区域，因此 三国的交点必不存在。又由于分割开两块区域的 中不包含 与 的颜色，因此 与 不同盟。

这样，情形3.2就归入到情形3.1中。

情形4 若 有5个邻国，一共4种颜色。由于抽屉原理，总有两个邻国颜色相同。不妨把5个邻国记为 ，其中只有 与 同色。

情形4可以划分为以下两种情形。

情形4.1 若 中存在两个国家不同盟。

不失一般性，假设 与 不同盟。那么将 所在的含 颜色的联盟反相之后，将会具有和 相同的颜色。此时将剩下一种颜色给 ，即可完成 的四色填充。

情形4.2 若 中任意两个国家之间都同盟。

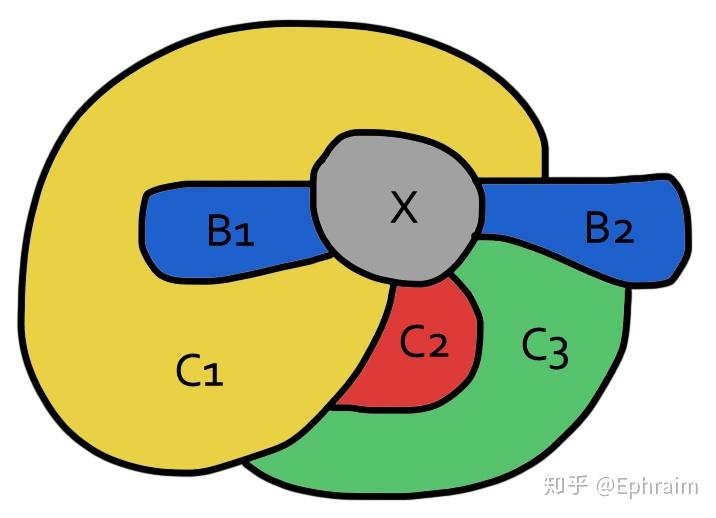
首先我们注意到，一定存在某个 ，使得 的三国交点不存在。

证：假设对于 ， 的三国交点都存在。由于 与 的任何一条邻边只能有两个端点，要使得这三个三国交点都存在于 的边界上， 与 至少有两条邻边。这表明 必然构成一个环形结构，分隔出至少两块互不连通却都与 相邻的连续区域 。由于在情形4.2中 里任意两两配对都属于同一个联盟，而这些联盟并不具有将两块区域分开的 中的颜色，所以都同属于两块区域的其中一块，不妨认为是 。
现在唯一的可能性是其他区域 与 的邻边由 完全占据。我们现在把整个连通区域 当成是一个国家，在这个意义下 只有4个邻国。通过情形3的结论我们知道，在4个邻国 中必然有两个国家不同盟。情形4.2中， 中任意两个国家都同盟，所以只能是 与 某一个 不同盟。但如果 与 不同盟，显然 的三国交点不能够存在了，与假设矛盾。

同样的，我们也能找到某个 ，使得 的三国交点不存在。

根据 与 是否相等，我们分情况讨论。

情形4.2.1 若存在不同的 与 ，使得与两个三国交点都不存在。

不失一般性，令 ，于是与两个三国交点都不存在。

根据 与 的联盟情况，把情形4.2.1划分成如下两种情形。

情形4.2.1.1 若 与 不同盟， 与 也不同盟。

此时只需把 所在的包含 颜色的那个联盟反相， 即变为 的颜色，把 原本的颜色给 ，就完成了 的四色填充。

情形4.2.1.2 若 与 或 中至少一个同盟。

不失一般性，假设 与 同盟。

我们将 所在的拥有 颜色的联盟记为 ，将 所在的拥有 颜色的联盟记为 。注意到 与 两个联盟不可能连通。

证：若是 与 连通， 会形成一个环状结构，必然可以划分出两块互不连通，却都与 相邻的区域 和 。因为 的环状结构中不包含 的颜色， 不能同时存在于 和 两个区域中。假设 ，那么 必不能同 中的 或 同盟。但这却是情形4.2所要求的，矛盾。

我们现在将 与 分别反相，则 变为 的颜色，而 变为 的颜色。原本 的颜色在 的邻国中不存在了。我们将这种颜色给 ，就完成了 的四色填充。

情形4.2.2 若不存在 ，使得与两个三国交点都不存在。

不失一般性，我们令，那么与两个三国交点都不存在。

同时，如果此情形不能包括在情形4.2.1中，那么必须承认，，，这些三国交点都存在。

我们来证明，同时满足这些条件的地图已经不存在了。下面的图示有助于理解证明的过程。

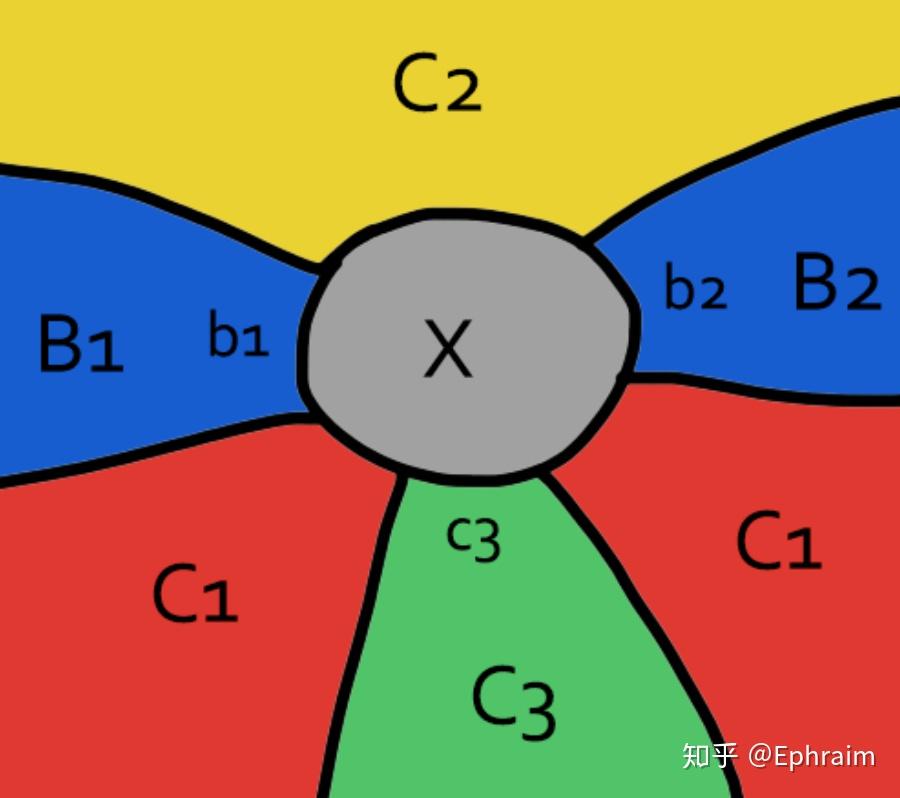
证：首先注意到 与 只能有一条连续的邻边。因为若是有至少两条邻边，则 必然形成一个环形结构，分隔出至少两块互不连通却都与 相邻的连续区域 。情形4.2要求若 中任意两个国家之间都同盟，那么它们必然同属于一个区域，假设是 。现在 若是属于 ，则没有其他邻国可以占据 了；若不属于 ，则 这样的三国交点不可能存在了。矛盾。
同样的道理，可以证明 与 只能有一条连续的邻边。
再注意到 与 也只能有一条连续的邻边。因为若是有至少两条邻边，则 必然形成一个环形结构，分隔出至少两块互不连通却都与 相邻的连续区域 。情形4.2要求若 中任意两个国家之间都同盟，那么 必然同属于一个区域，假设是 。现在 若是属于 ，则与 的邻边只能由唯一剩下的 占据，则 这样的三国交点不可能存在；若不属于 ，则 这样的三国交点不可能存在。矛盾。
我们证明了 与 各自都只能有一条邻边，不妨记为 。由于，，，这些三国交点都存在，所以 的两侧必须分别是 和 ， 的两侧也必须分别是 和 ，但由于 占据了一段 的边界线，我们可以断言 和中至少有一个与 有两条邻边。不妨认为是 。
那么现在则 必然形成一个环形结构，分隔出至少两块互不连通却都与 相邻的连续区域 。情形4.2要求若 中任意两个国家之间都同盟，那么 必然同属于一个区域，假设是 。现在 若是属于 ，则与 的邻边只能由唯一剩下的 占据，则 这样的三国交点不可能存在；若不属于 ，则 这样的三国交点不可能存在。矛盾。

至此我们证明了，只要四色定理对 个国家的地图成立，那么对任何包含 个国家的地图，总可以找到一个国家 拥有不超过5个邻国。经过对一些联盟进行反相操作，我们总可以使得所有邻国的颜色总数降为3个，从而把剩下一种颜色给 完成 的四色填充。

因此，四色定理对任何有限个国家的地图都成立。

如果你一路跟下来读完了，请给自己一点掌声（答主写都快写晕了）。毕竟这可能是你第一次正儿八经挑战数学难题中的大BOSS。

然而就和其他所有你打过的BOSS一样，并不是看起来血条打空了它就真的乖乖地死了。聪明的你能够发现证明里某个情形下的小小漏洞，举出一个反例来，作为开启隐秘之门的钥匙，打开需要无数勇士探索长达一个世纪之久的，藏着一切守卫、机关、和恶龙真正本体的地下宫殿吗？

好了我知道你找不到。。不然也不至于骗过全世界11年。看吧，钥匙长这样，拿着它，你回头能发现证明错哪了吗？