岭回归和最小二乘法的区别是什么?什么时候比较适合用岭回归?
本文讲下岭回归,还是从三个方面讲述
1、什么是岭回归?
2、为什么要用岭回归?
3、代码实现过程
1、什么是岭回归以及为什么要用岭回归
通俗地讲,可以把岭回归看做是普通线性回归的一种优化,它是通过引入L2正则化项来对模型进行优化,最终使模型的拟合效果更好。
之所以要这样做,是因为普通线性回归模型,我们前文提到的,其求解模型参数的思想是根据最小二乘法求解,即
参数
而这样的求解,在有的时候会出现问题,当自变量间存在多重线性关系或者矩阵不可求逆时,这种求法就会出错或者是参数K会很大。
于是,就在线性回归模型的目标函数上引入l2正则项(也叫惩罚项),最终的目标函数为:
,
为回归系数,
则为正则项平方的系数,为非负数
然后对目标函数进行求导,最终结果为:
当 ,该目标函数就跟普通线性回归模型的参数一样;当
,参数就会趋近于0。
所以岭回归模型中, 值的确定也是非常关键的,它不是随机给的值,是可以通过一系列方法求出来的。python自带的Ridge类,默认的值是为1的。下面我们将下两种确认
值的方法。
方法一:岭迹分析
顾名思义,就是结合模型参数,随着 值逐渐增大,看参数最终都稳定下来时,
值的大概范围。
方法二:交叉验证法
将数据集拆分成K组,选K-1组作为训练数据,1组作为测试数据,以此会得到k种训练集合测试集,对每一个给定的 值计算MSE(平均均分误差),找到最小的MSE,并将其对应的
值找出来。
下面,我们将通过python自带的函数来实现。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings('ignore')
#导入我们的数据
salary=pd.read_excel(r'C:\Users\83687\Desktop\salary.xlsx')
salary.head()
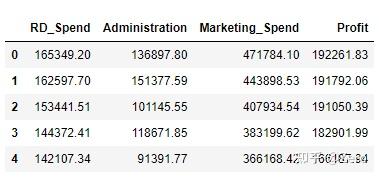
如上图,总共有三个自变量RD_Spend、Administration、Marketing_Spend,因变量为Profit,我们先看下变量间的关系,先用可视化看下
sns.pairplot(salary)
plt.show()
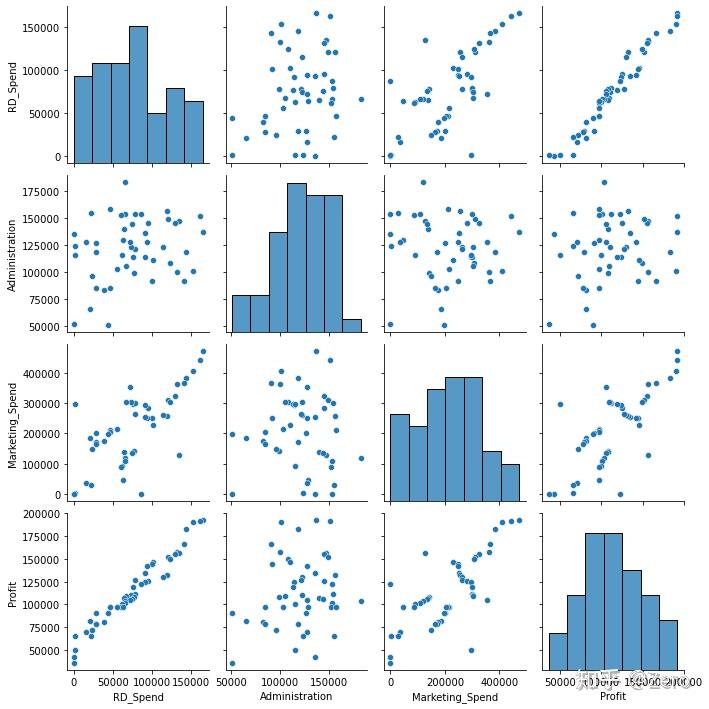
由图可知,RD_Spend和Profit存在明显线性关系,同时RD_Spend与Marketing_Spend亦有一定的线性关系,接下来我们算下变量间的相关系数。
for i in salary.columns:
print('{}与其他变量的关系'.format(i))
print(salary.corrwith(salary[i]))
结果:
RD_Spend与其他变量的关系
RD_Spend 1.000000
Administration 0.243438
Marketing_Spend 0.711654
Profit 0.978437
dtype: float64
Administration与其他变量的关系
RD_Spend 0.243438
Administration 1.000000
Marketing_Spend -0.037280
Profit 0.205841
dtype: float64
Marketing_Spend与其他变量的关系
RD_Spend 0.711654
Administration -0.037280
Marketing_Spend 1.000000
Profit 0.739307
dtype: float64
Profit与其他变量的关系
RD_Spend 0.978437
Administration 0.205841
Marketing_Spend 0.739307
Profit 1.000000
从相关系数看,跟我们看图的结果是差不多的,RD_Spend和Profit相关系数达0.97,RD_Spend与Marketing_Spend的相关系数也有0.71。
接下来我们用岭回归实现拟合下。
from sklearn import model_selection #将数据划分训练组和测试组
x_train,x_test,y_train,y_test=model_selection.train_test_split(salary[['RD_Spend','Administration','Marketing_Spend']],salary['Profit'],
test_size=0.2,random_state=1234)
#这里求最优的λ值用的是交叉验证法
ridge_cv=RidgeCV(alphas=Lambdas,normalize=True,scoring='neg_mean_squared_error',cv=10)
ridge_cv.fit(x_train,y_train)
ridge_best_lambda=ridge_cv.alpha_
print(ridge_best_lambda)
#用最优的λ值来搭建岭回归模型
linear3=Ridge(alpha=ridge_best_lambda,normalize=True)
linear3.fit(x_train,y_train)
print(linear3.coef_)
pred2=linear3.predict(x_test)
MSE2=mean_squared_error(pred2,y_test)
print(MSE2)
plt.scatter(pred2,y_test)
plt.show()
结果:
1e-05
[ 0.8 -0.06 0.01]
84334440.11945987
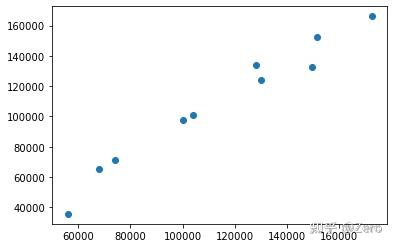
结果发现, 值为
,已经很接近0了,如前文所说的,当
值很接近0时,其就相当于常规线性模型,我们引入常规线性模型,看下效果,做个对比
linear1=LinearRegression()
linear1.fit(x_train,y_train)
print(linear1.coef_)
pred1=linear1.predict(x_test)
MSE1=mean_squared_error(pred1,y_test)
print(MSE1)
plt.scatter(pred1,y_test)
plt.show()
结果:
[ 0.8 -0.06 0.01]
84336820.72037044

从参数上看,跟岭回归模型算出来的基本一致,从均分误差看,岭回归模型略低于常规线性回归模型,效果略微好那么一丢丢。
可能是例子的问题吧,没能很好的展示出岭回归和常规线性模型的差异,不过实际业务中,其实很少使用常规线性模型的,要么用岭回归,要么Lasso,要么梯度下降。
那本章内容就到此结束,下章我们再学习Lasso。