为何游戏引擎决定画质?
渲染计算的三大组成部分
- 光照
- 材质
- 着色

渲染方程及挑战
渲染方程式
1986年,元老级人物James Kajiya提出了渲染方程式,这一方程可抽象概括所有的渲染计算。

渲染方程式表明:经过任意点x反射到观察点中的辐射通量由x点自身发光和其他点反射到x点的辐射通量组成,其中其他点反射到x点的光照又可分为直接光照和间接光照。

渲染方程在实际运用中非常复杂,包含诸多影响因素。
具体分析可参考大佬的文章:王江荣:路径追踪(Path Tracing)与渲染方程(Render Equation)
挑战一
阴影(Shadow)是我们判断物体空间关系的重要条件,我们该如何模拟出真实的阴影呢?
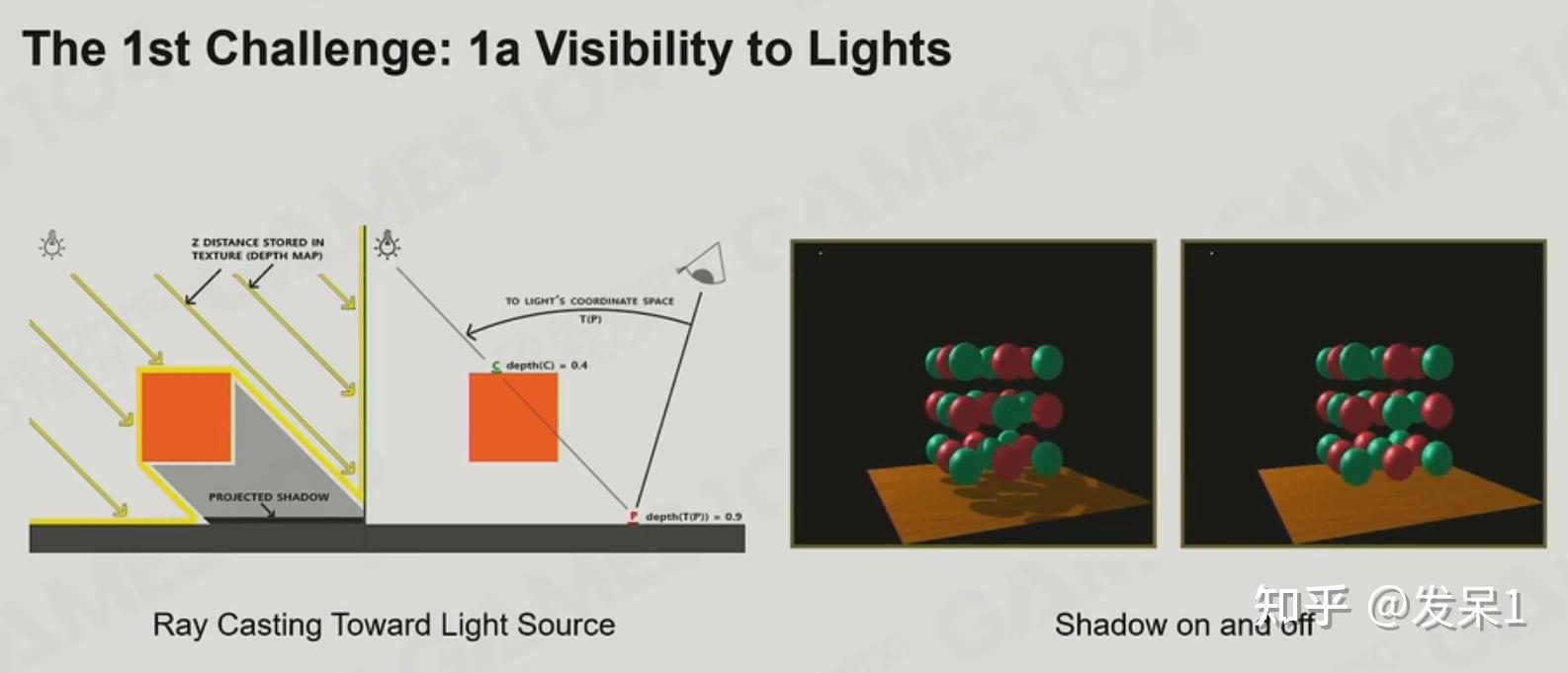
光源的复杂性,光源有点光源、方向光源、面光源等不同种类,在实际应用中光照强度也有所不同。

radiance指光照射到物体上反射出的能量;而irradiance则指入射的能量。
挑战二
如何高效的对双向反分布函数(BRDF,Bidirectional Reflectance Distribution Function)和入射辐射率的乘积进行积分,这里可以使用Monte Carlo积分(在上面大佬的文章中也有具体分析)。

挑战三
因为光可以反射,所以全局范围内任何一个物体都可以作为光源,即一束Output的光下一次可能作为Input输入,这样形成了一个递归的过程,典型案例Cornell Box。

总结一下三个挑战
- 对于任一给定方向如何获得irradiance
- 对于光源和表面shading的积分运算
- 对于入射光和反射光不断递归过程的计算

简易光照解决方案
光源的简化
我们使用方向光源、点光源、锥形光源等作为Main Light,取Ambient Light作为除主光外的环境光的均值,以此简化复杂的计算。

对于能够反射环境的材质,我们可以设计一种环境贴图,通过采样环境数据来表现

材质的简化
基于一个光照可以线性叠加的假设(在渲染方程式中也有用到),Blinn-Phong模型通过叠加Ambient(环境)、Diffuse(漫反射)、和Specular(高光)来简单粗暴的描述材质的着色计算

当然,Blinn-Phong模型也有缺陷。
能量不保守,使用Blinn-Phong模型的出射光照能量可能大于入射光照的能量,这在计算光线追踪时会带来很大的问题:这一过程在光线追踪中经过无限次反弹后,会使得本该暗的地方变得过于明亮。
难以表现真实的质感,Blinn-Phong模型虽然比较经典,但它却很难表现出物体在真实世界中的模样,总是有一种”塑料“感。

阴影的简化
Shadow简单说来就是人眼可见区域中,光线无法照到的地方。在过去十几年中,对于Shadow最常见的处理方式便是Shadow Map
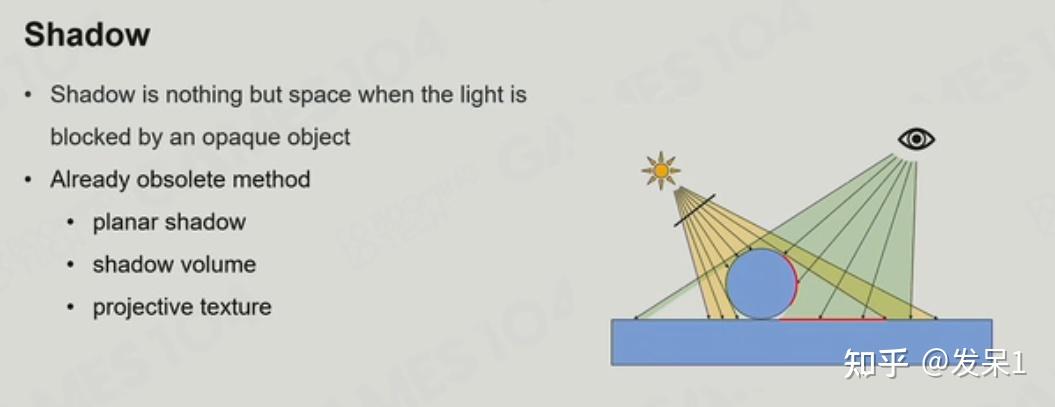
Shadow Map的思想可以简单概括为:第一次先在光源处放置相机,以z-buffer的方式储存一张对应的深度缓冲,第二次将相机放置在观察的位置,并将视锥内的点的深度和深度缓冲中的对应点(三维坐标转换为二维坐标后,在平面坐标系中对应的点)的深度进行对比,若前者大于后者,则认为视锥中的点处于阴影中
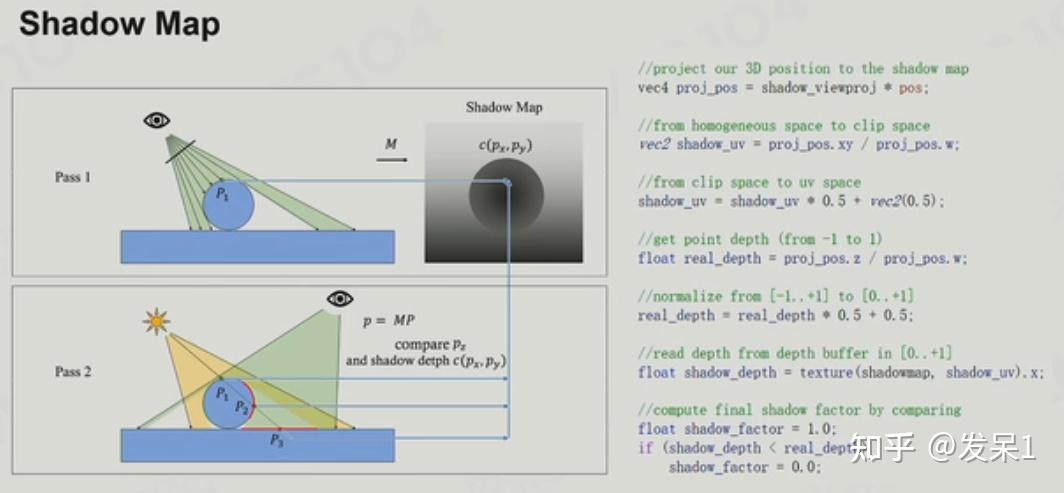
Shadow Map在使用时也会出现问题,光源处的采样率和观察处的采样率不一样,会出现走样,最经典的就是处理精细结构时的自遮挡问题

到这里我们就实现了对于三个挑战的一个简易光照解决方案

基于预计算的全局光照
只用直接光照会使得场景的平面感很强,而使用全局光照(直接光照+间接光照)能很大程度上的还原真实情况

如何表现全局光照
- 我们需要储存数以万计的光照探测器,因此我们需要一个很好的压缩比率
- 材质的BRDF卷积运算涉及到复杂的多项式积分运算,我们需要利用数学方法简化积分运算

卷积定理(Convolution Theorem)
百度百科:卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出,函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理,时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积,两者具有对偶关系。
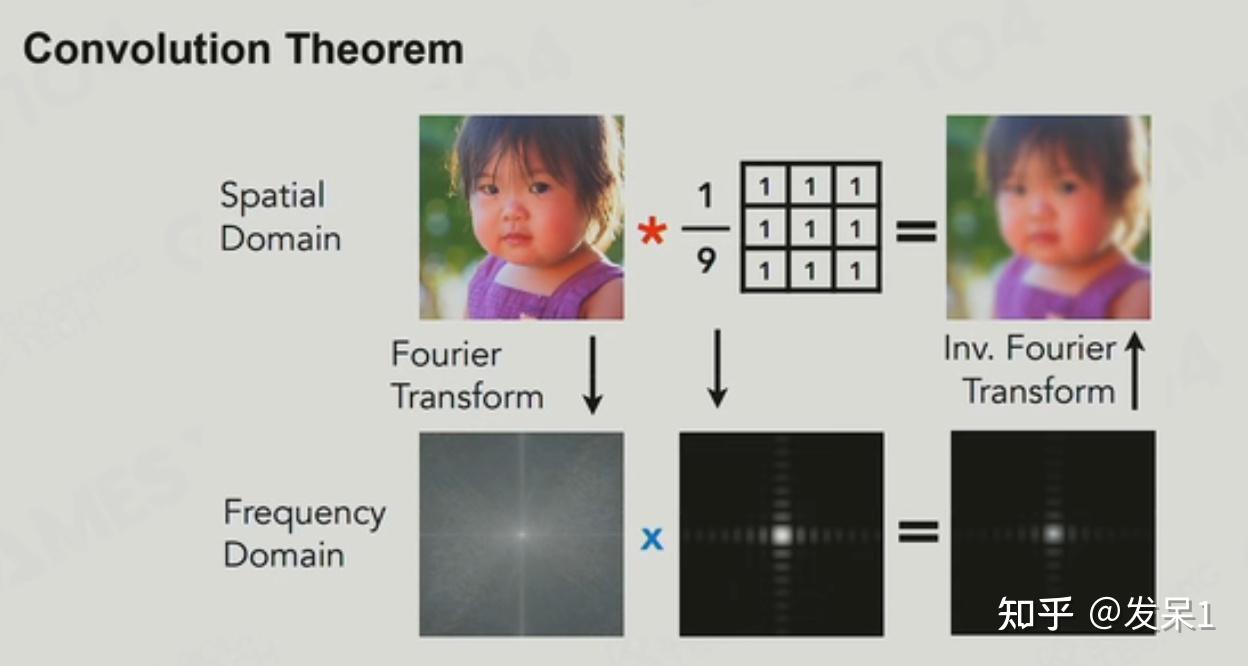
对于空间域中的一个数字信号(下图以照片为例),我们可以通过傅里叶变换将其转化为频率域的一段频率,截取频率的一小段就可以实现对频率整体的一个粗糙的表达,这时我们再通过反向傅里叶变换就可以得到原数字信号的大概情况。通过这一数学性质,我们不需要再去进行复杂的乘积累加和运算
球谐函数(Spherical Harmonics)
球谐函数就是一组基函数的集合,并且基函数越多,它的表达能力就越强(我个人理解就是回归性越强)
球谐函数有以下性质:
- 正交性,这些基函数卷积在一起时值为0
- 球谐函数的二阶导数为0,它的图像变换是光滑的
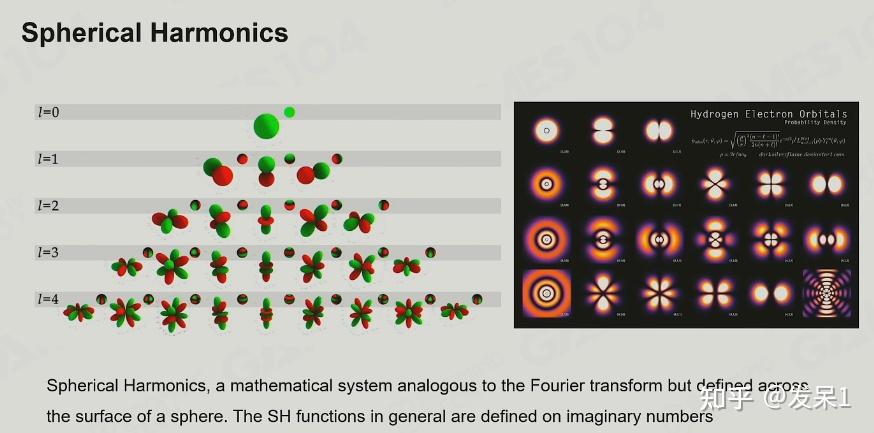
使用球谐函数,我们就可以通过一阶多项式近似的表达一个球面光照(低频信号)
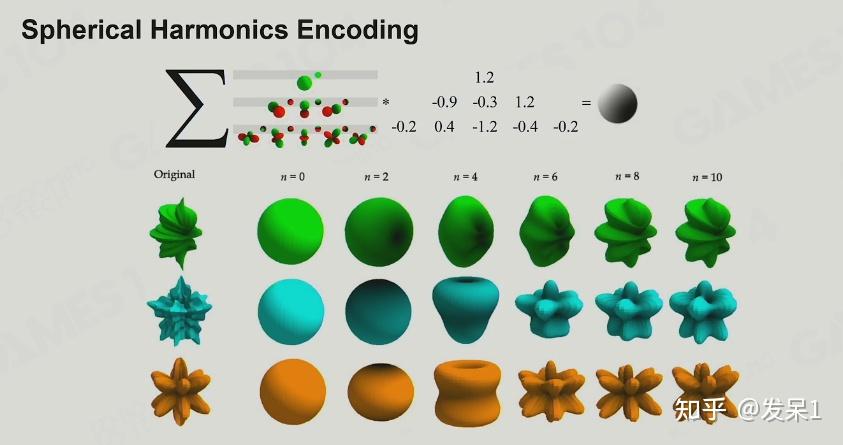
Lightmap
有了球谐函数这一便捷工具,我们就可以将许多几何物体拍下存放在一张贴图上(这张贴图通常被称为“atlas”),这一过程又分为几个步骤
首先我们需要将几何物体进行简化,而后在参数空间内为每个几何物体分配近似的texel精度

下面我们在场景内加入全局光照,就可以表现出非常真实的效果

相应的,使用Lightmap有以下优缺点:
- Pros:1.实时运行效率很高;2.可以表现出全局光照的许多细节
- Cons:1.漫长的预计算时间;2.只能处理静态的场景和静态的光照;3.内存换时间,占用空间较大

Light Probe
我们可以在空间内放置许多采样点,对于每个采样点采集其对应的光场,当有物体移动经过某一采样点时,通过寻找附近的采样点并计算插值,就可以得到该采样点的光照

那么这么多的采样点我们该如何生成呢?我们首先在空间内均匀的产生采样点,再根据玩家的可到达区域和建筑物的几何结构进行延拓,相对均匀的分布采样点
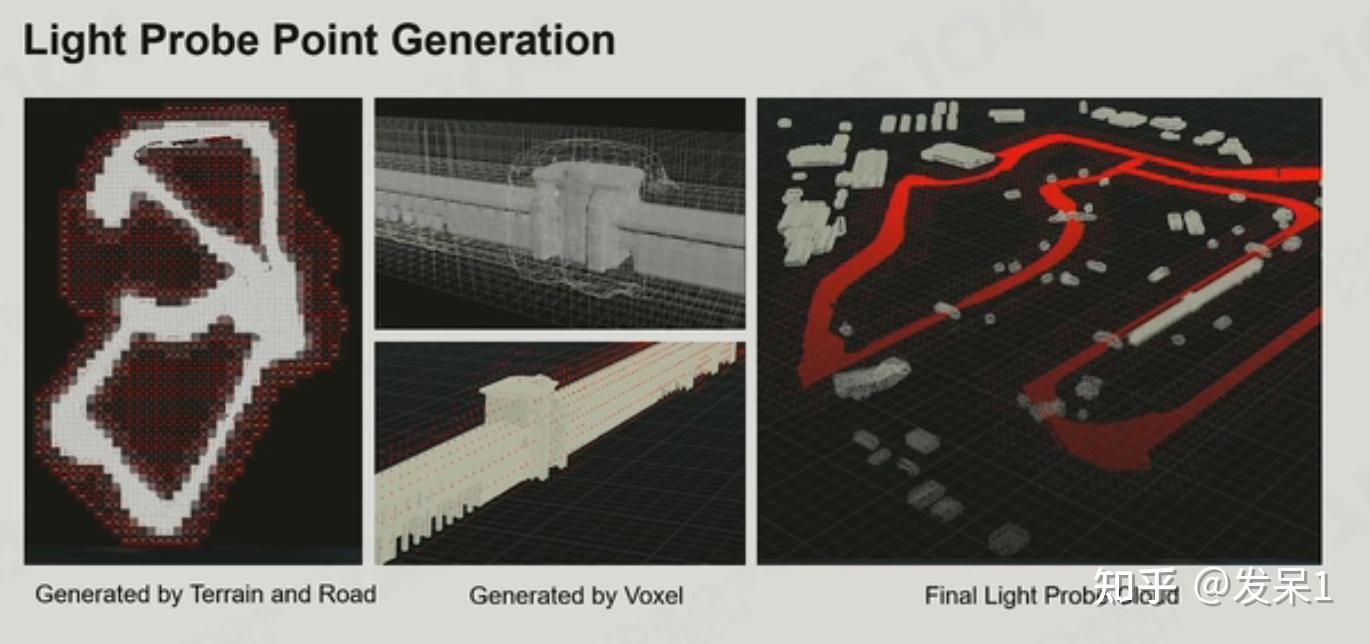
Reflection Probe
我们还会做一些数量不多但采样精度非常高的Reflection Probe用于表现环境,一般它们与Light Probe分开采样

综合使用Light Probes和Reflection Probes,我们已经可以实现一个不错的全局光照的效果,它给我们带来以下好处:
- 实时运行效率很高
- 既可以处理动态物体又可以处理静态物体,并且可以实时更新
- 既可以处理漫反射也可以处理镜面着色
当然它也有一些缺陷:
- 大量的Light probes需要我们进行预计算
- 相比于Lightmap,它对于全局光照和重叠部分的软阴影的细节处理精度较低

基于物理的材质
微平面理论(Microfacet Theory)
这一理论的思想可以概括为:一个平面表面的光滑程度取决于它的法向量的聚集度,法向量全都集中在一起时,它的反光就相对较好
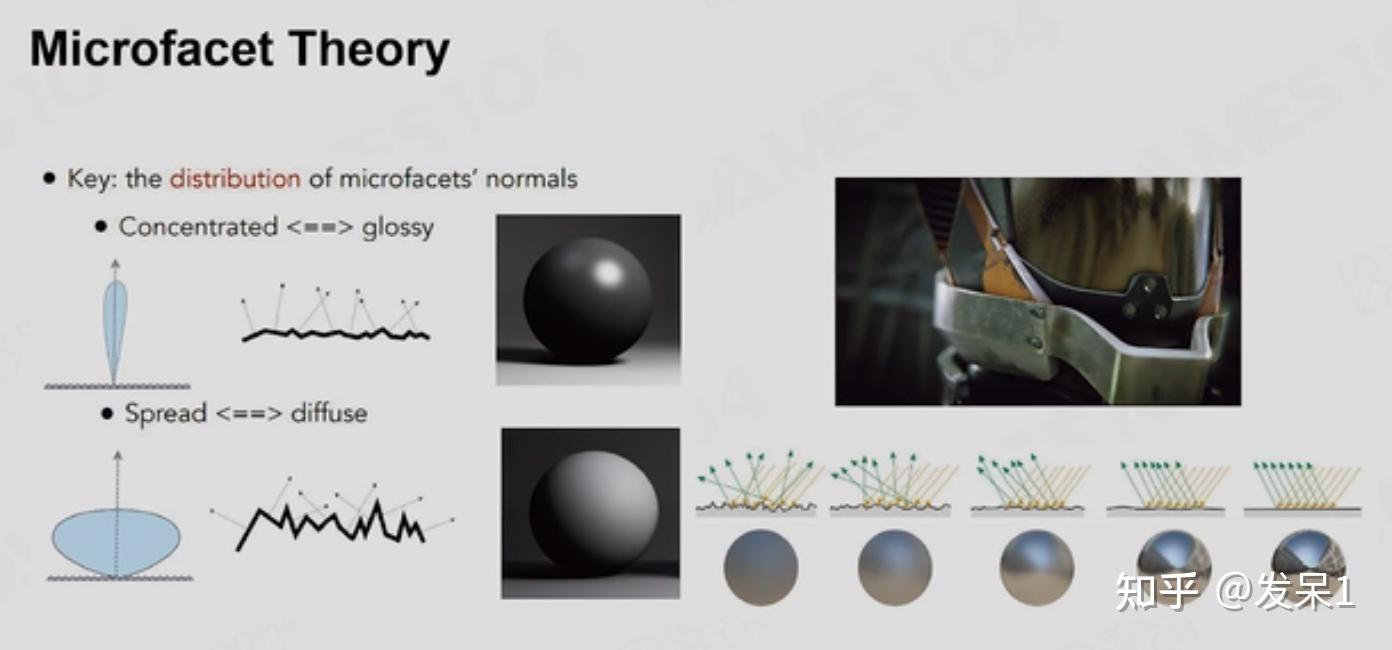
基于微平面理论的BRDF模型
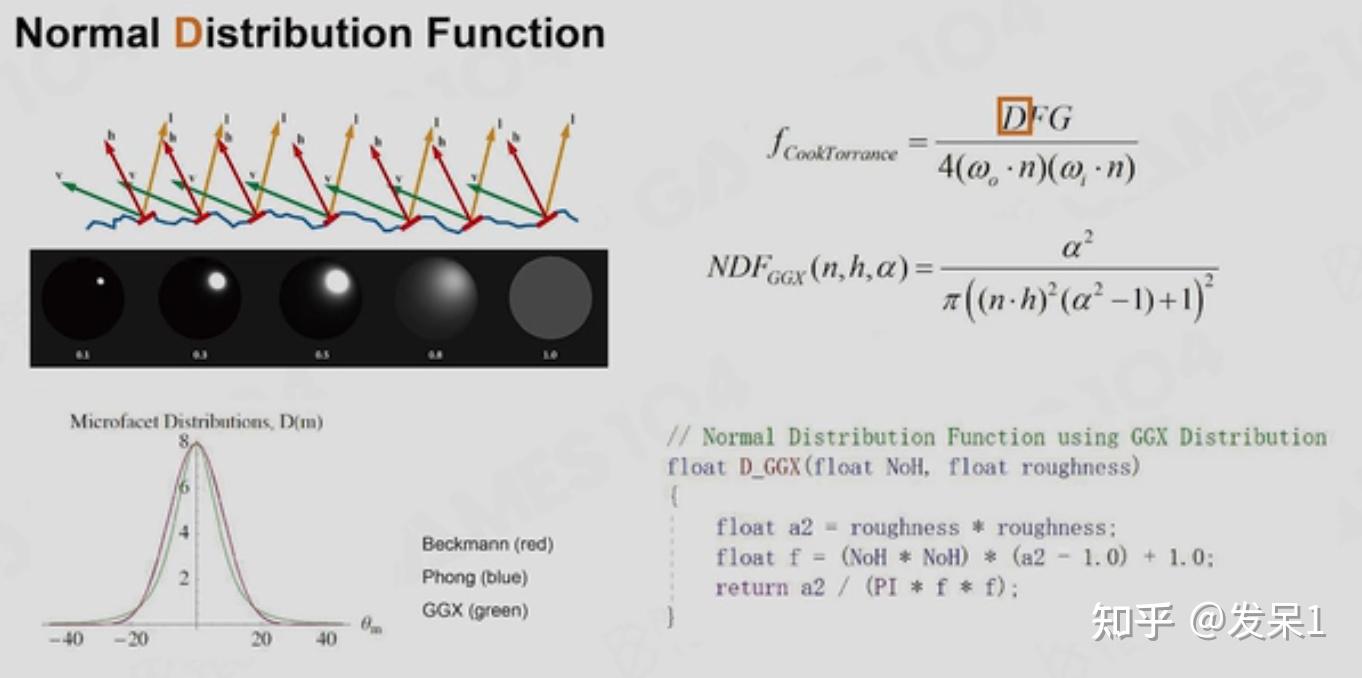
通过微平面理论我们可以将BRDF分为两部分,一部分是漫反射(diffuse)(这一部分的积分值为c/Π,c取决于入射的能量),另一部分则是高光(spectual),在该部分中引入了CookTorrance模型,其中DFG模型是CookTorrance模型中的核心元素。漫反射和高光的区别在于材质是金属还是非金属,金属中的电子能够吸收光子,它的高光就比较明显;而非金属中的电子不能吸收光子,光子只能在其内部进行一系列的漫反射

DFG模型中的D指法向分布方程(Normal Distribution Function)、F指菲涅尔现象(Fresnel Equation)、G指微表面几何内部的自遮挡(Geometric attenuation term)


MERl BRDF
为了便于艺术家们的使用,引擎工作者们对大量现实物体采样,构造出了MERL BRDF数据库,其中包含大量材质的BRDF参数

Disney BRDF Principle
- 使用的物理材质参数应当直白易懂
- 材质参数应当尽可能的少
- 参数取值范围尽量由0到1
- 各种参数的组合应当合理且有意义

PBR主流模型
Specular Glossiness(SG),这个模型中Diffuse控制漫反射部分,Specular控制菲涅尔现象,Glossiness控制材质的光滑程度。这一模型的参数设置较少,便于艺术家们使用,但也因其过于灵敏而容易导致奇怪的现象

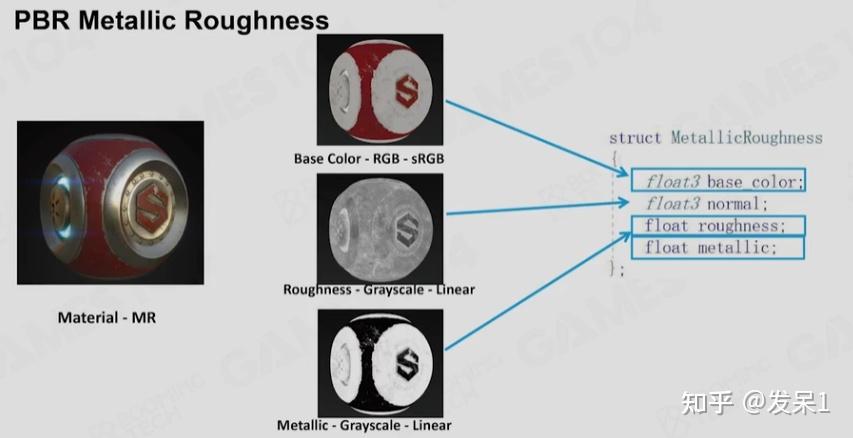
Metallic Roughness(MR),这一模型中首先设置一个Base Color,而后通过金属度(Metallic)来控制Diffuse和菲涅尔现象。仅调节金属度虽然使得灵活度下降了,但却不容易出问题,这也使得MR模型现今被更多的使用
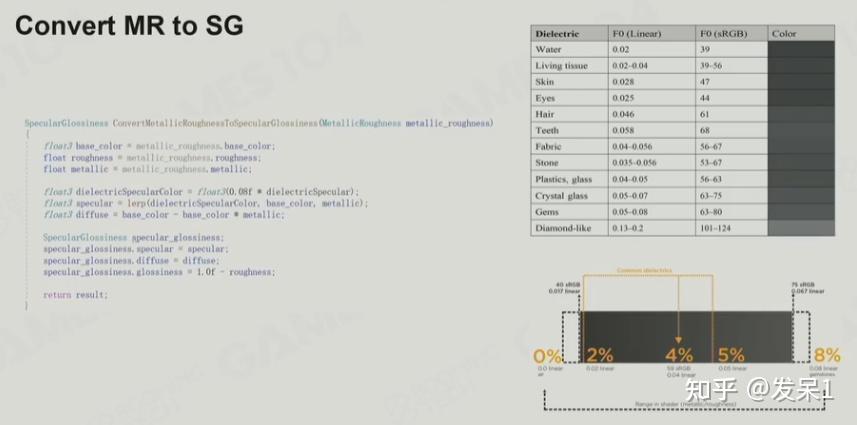
我们可以从MR模型转换为SG模型
下图为MR模型和SG模型优缺点的对比

Image-Based Lighting(IBL)
IBL的核心思想是:若我们能对环境光照的信息进行一些预处理,是否能减少光照处理中积分运算消耗的时间

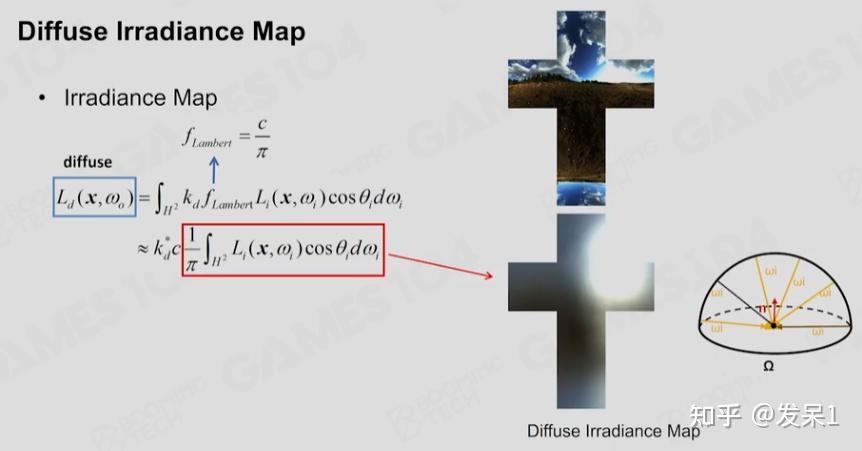
对于漫反射部分的光照,我们可以预先进行对应的卷积运算,并将其储存在Irradiance Map中
对于Specular部分,它涉及大量复杂的计算,可以近似为Lighting Term和BRDF Term的乘积

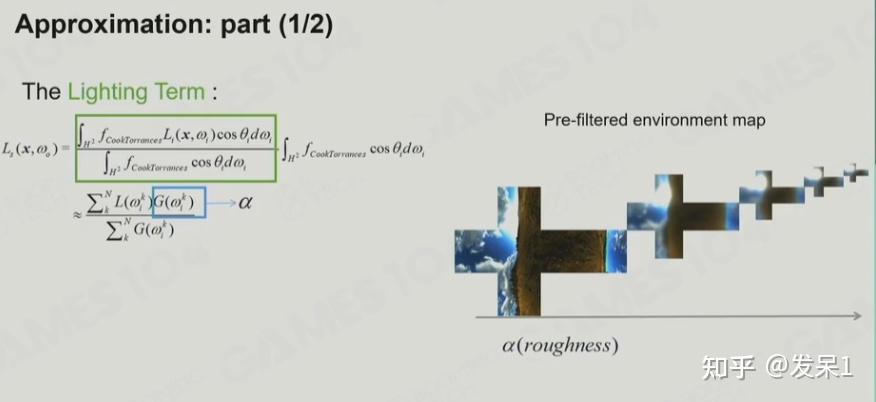

听到这里已经懵逼了,这一节课好难QAQ,先在这里留个坑,等把其他知识补了再回来填……
课程传送门:05.渲染中光和材质的数学魔法 | GAMES104-现代游戏引擎:从入门到实践_哔哩哔哩_bilibili