如何理解最小作用量原理？

发布时间：

2023-08-15 23:37

阅读量：

自然在产生其效果时，总是选择最简单的手段......它所选取的途径是作用量的值最小的那个。
——【法】莫培督

许多年后，面对纸上量子力学的路径积分，费曼先生将会回想起，巴德老师为他介绍那个“奇迹”时的下午。

他只是解说，他并没有证明任何东西，没有任何复杂的事情，他只是说明有这样一个原理存在。我随即为之倾倒，能以这样不寻常的方式来表达一个法则，简直是个不可思议的奇迹。
亲爱的巴德先生：您当然知道如何最大限度地将一个年轻男孩的智力伸展到成就的顶点......而且您还懂得如何掌握（请原谅我的不礼貌）一名超常的学生。

到底是什么令一代物理宗师费曼倾倒，并穷其一生去探索其奥秘。现在我们正式进入本节内容：最小作用量原理。

（一）费马原理

（1）希罗最短路径原理

希罗（Hero of Alexandria）是一位古希腊的数学家和工程师，希罗根据古希腊人对自然法则的理解：大自然总是遵循最简单的和最经济的准则在运行。他想：光也是大自然的产物，那么光的路径如何才能最简单直接呢？路径最短！所以他在他的著作《反射光学》中提出了光线的最短路径原理，被称为希罗最短路径原理。

图来自维基百科

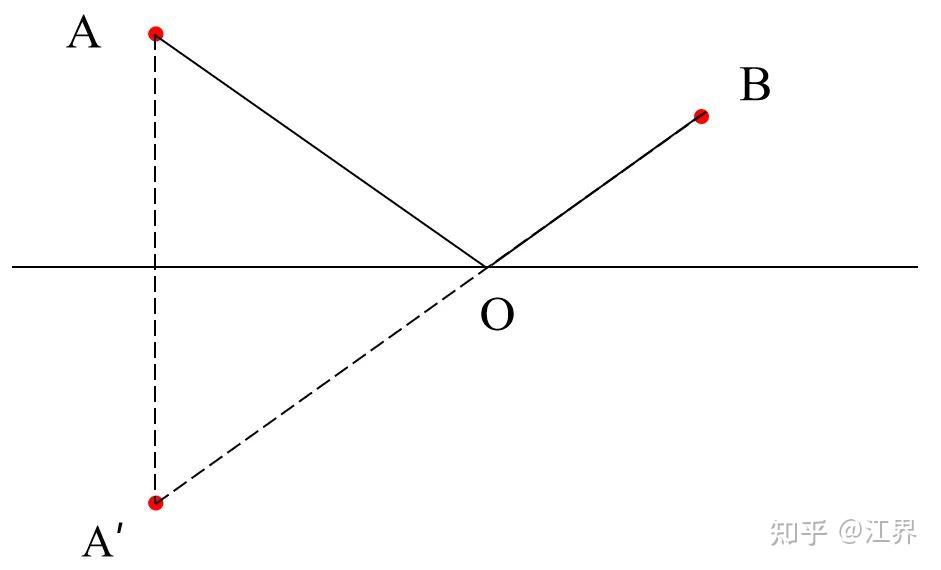
和我们初中学过的将军饮马问题类似，A和B点分居直线两侧，如果想求从A到B的最短距离，只需要作A的对称点A'，连接A'B交直线于点O，那么AOB就是最短距离，根据希罗最短路径原理，这就是光的反射路径，显然他的论证是成功的，因为我们初中学过，反射角等于入射角，反射光线、入射光线分居法线两侧，且三条线在同一平面内，希罗最短路径可以很好的说明上述三条。

但是接下来问题出现了，对于光在介质中的折射，按照最短路径，显然是两点间直线最短，但是实验得出了不同的结果，如图为在水表面的折射和反射，光从空气到水中走过的路径并不是直线，那该如何解释呢。

图片来自维基百科

（2）胡不归问题

在解决折射问题之前，我们先卖个关子，来讲一个小故事。

话说很久很久以前，有一位书生，远赴异乡上京赶考，在遥遥路途中，夜里他经常望着月亮，吟诵着李白的“举头望明月，低头思故乡”。是的，远离故乡使得他倍感羁旅之思，更重要的是，家里还有一位病重的老父亲。这天夜里，正当他望着月亮出神，眼里泛着泪花时，突然一个人闯进了他的房间，定睛一看，这不是村头的李小二吗，他怎么来了？
“江大哥，你父亲快不行了，他托我带你回去，他想再见你一面啊。”听到这，江书生心头一颤，顿时腿软了三分，硬挺着不瘫倒在地上。过了一会，缓过神来，他又好像着了魔一样，把床头上的书卷囫囵丢到竹筐里，背上就往外跑，边跑边喊着：
“快走！我们回去！”

于是这位书生和李小二一起连夜向家里赶，但是现在他们面临着一个关键的问题——如何以最短时间回到家。

第一象限部分表示砂砾地，x轴表示驿道

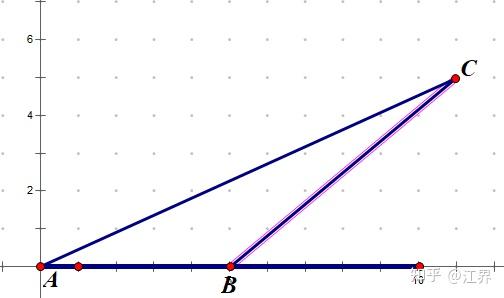
如图所示，他们身处A点，家在C点，AB方向为驿道，AB上部分为沙砾地，他们在驿道行走的速度要比沙砾地快，书生看着手上的地图，心想：小学生都知道两点之间线段最短，听我的，走AC这条路。

结果走到距家几里地的时候，书生突然心中梗塞：不好，来不及了。等到他们到家时，老父亲已经过时，村里的乡亲们说，他在弥留之际还喊着“胡不归，胡不归......”。

试想，如果书生走的不是AC路径，结果会不会不一样。下面我们就来讨论一下这个问题。

书生并没有找到最短时间的路径，他找到的只是最短的路程，但是由于AB段的时间比AC段快，所以实际上最短时间的路径要求我们先沿着AB走一段路程，在由B到C，我们接下来的任务就是寻找B点，下面提供三种解法：

①等效路程法：我们假设C点坐标为 $（x，y）$ ，书生在驿道的速度为 $v_{1}$ ,在沙砾道的速度为 $v_{2}$ ，且有 $v_{1}＞v_{2}$ ，假设书生在驿道上走过的路程为 $s_{1}$ 那么，我们可以根据速度关系等效为在沙砾道走过的路程 $s_{1}'=\frac{v_{2}}{v_{1}}s_{1}$ ，等效路程意味着改变出发点，但时间不变。

等效出发点记作A'，时间最短意味着A'BC为直线

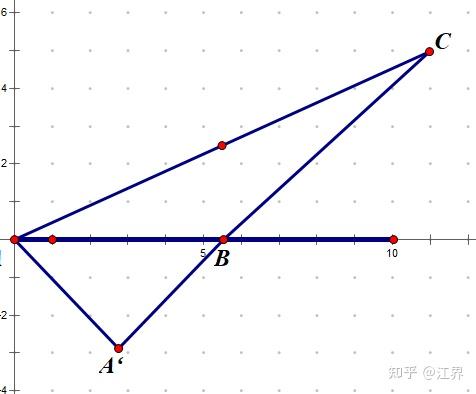
如图所示，我们将等效的出发点记作A'，那么有关系

$\frac{\left| A'B\right|}{\left| AB\right|}=\frac{v_{2}}{v_{1}}$ , $sin\angle BAA'=\frac{v_{2}}{v_{1}}$

此时我们将A'点固定，所以问题化作何时A'BC路程最短，两点之间线段最短，所以B点位置为

$x-ytan\angle BAA'=x-y\frac{v_{1}}{\sqrt{v_{2}^2}-v_{1}^2}$

②包络线法：在经过时间t后，我们来考察书生走过的路径范围。如果书生不沿着驿道走，那么他走过的路径范围应当是以A点为圆心的一个圆，如果书生沿着驿道走过一定路程，那么他走过的路径范围应当是圆心在驿道上某一点的圆，现在让书生不断地沿驿道走，画出一个又一个圆，你会发现，这些圆的边界会形成一条直线，我们称之为包络线，如图所示，他表征了经过t时间后，书生走过的最远路程的边界范围。

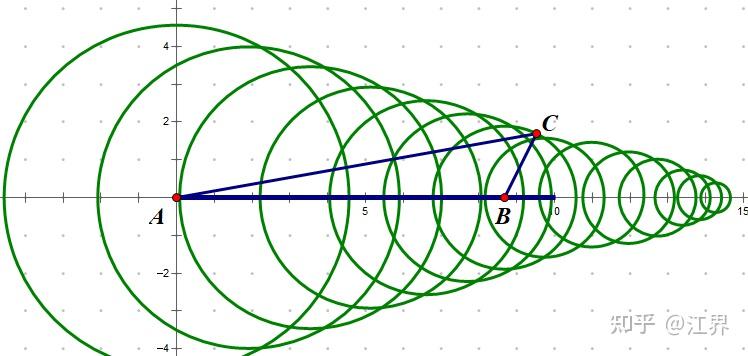
注意我们取的是某一特定时刻t的路径范围，即所有圆内的点他均可能到达，但是我们关注的是他可能到达的最远范围。

不难发现书生在驿道上走过的最远距离为 $v_{1}t$ ,在沙砾地走过的最远距离为 $v_{2}t$ ，那么其构成的包络线如下图所示

当包络线经过C点时，意味着时间最短

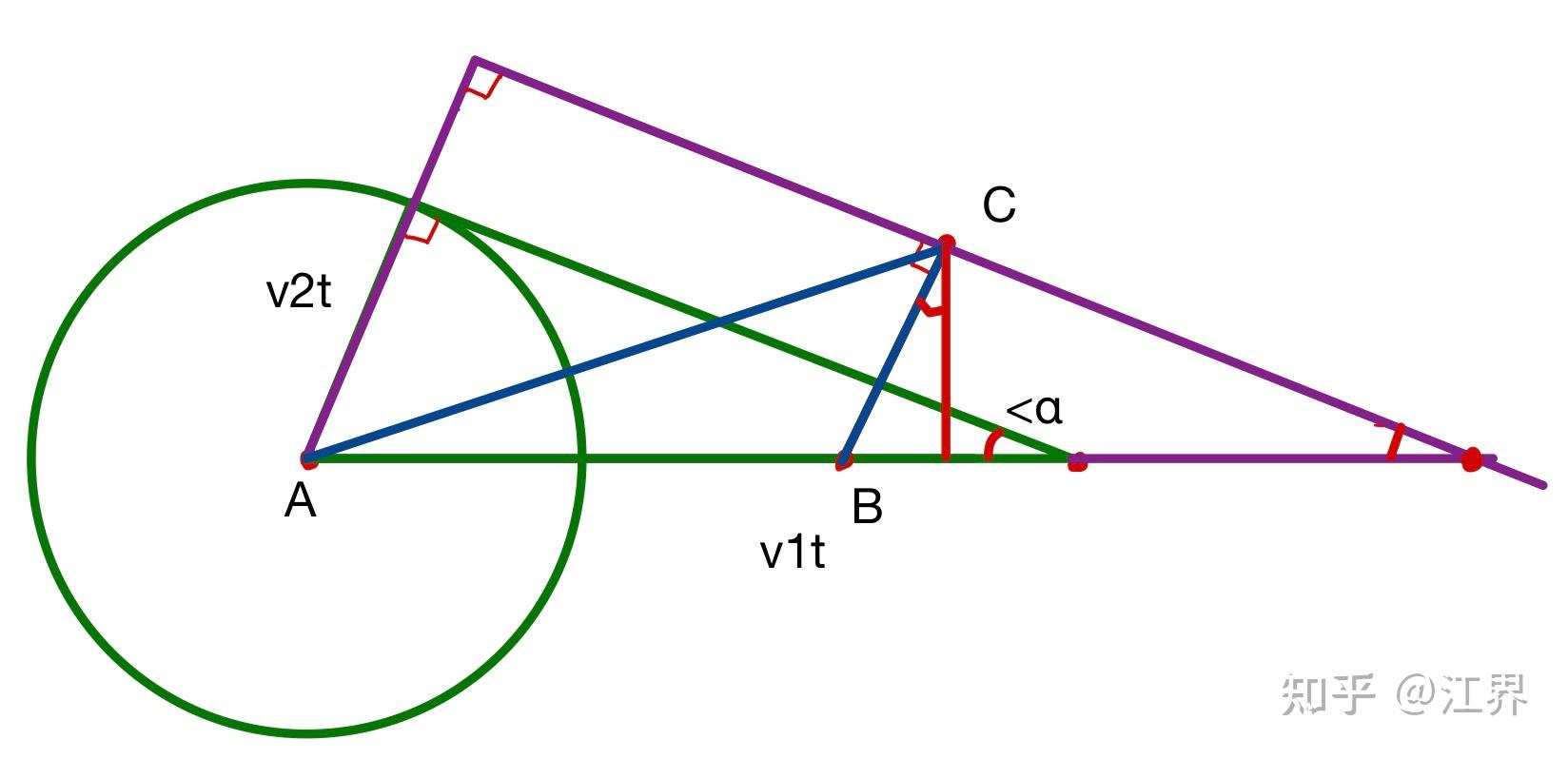
当包络线经过C点时，意味着此时时间最短，我们有 $sin\angle \alpha =\frac{v_{2}}{v_{1}}$ ,同样可以得到B点坐标 $x-y\frac{v_{1}}{\sqrt{v_{2}^2}-v_{1}^2}$

③极值法：假设我们已经知道了B 点的位置，那么如果我们写出t关于B点位置的函数，在B附近dx处取一B'点，那么在一阶小量的近似下，时间t趋于不变，由此我们就可以确定B点的有关信息。

在一阶小量的近似下，B和B'点对应的时间t并没有什么区别

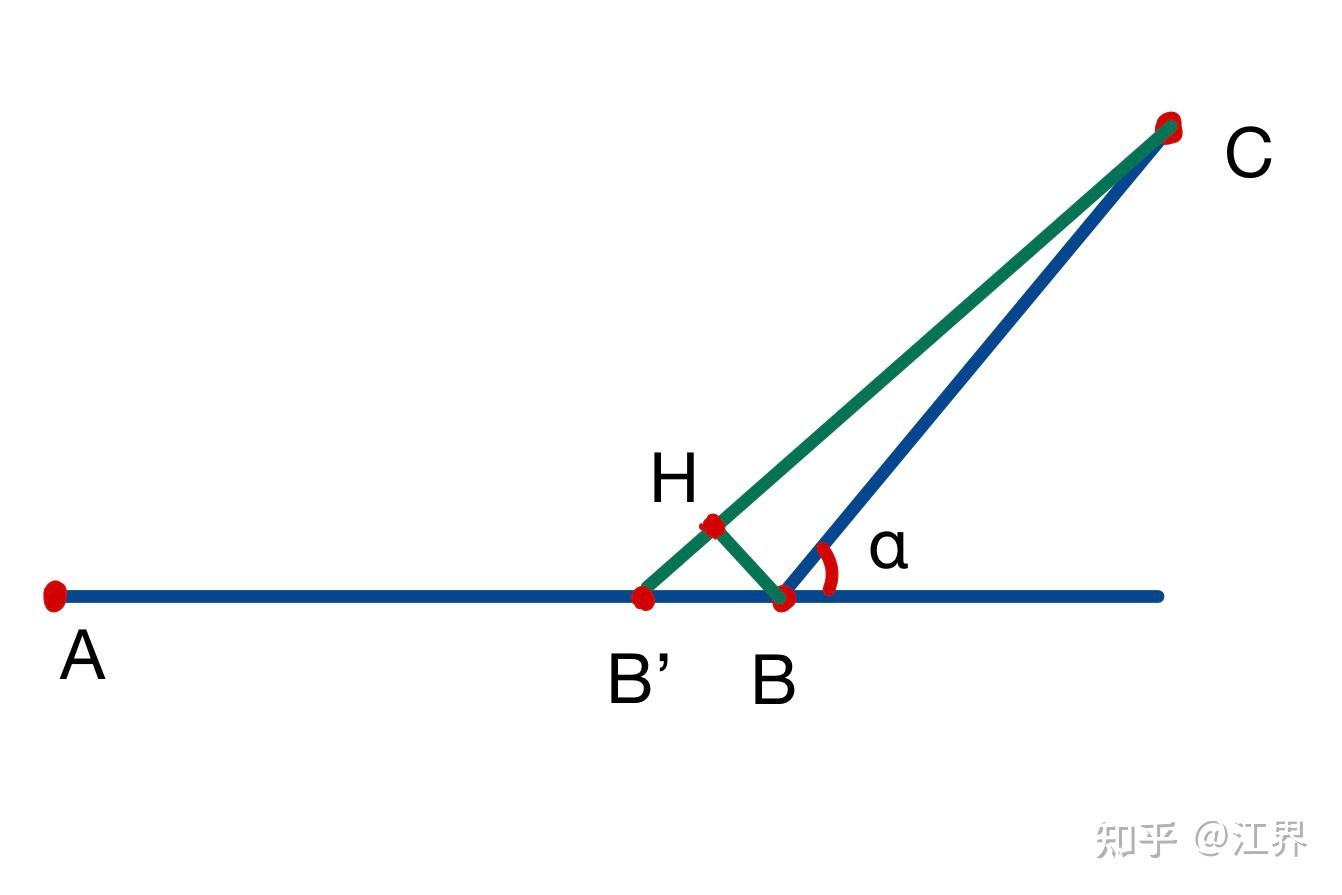
如图所示，取B'点，使得 $BB'=dx$ ,过B 做垂线BH，那么由于 $BC\approx CH$ ，B'点与B点所带来的时间差异集中在BB'和BH两边上，那么由B点的时间极值性质，两段的时间差异应当为0，于是我们得到 $\frac{dx}{v_{1}}=\frac{dx cos\alpha}{v_{2}}$

$\frac{v_{2}}{v_{1}}=cos\alpha$ ,同样可以得到B点坐标 $x-y\frac{v_{1}}{\sqrt{v_{2}^2}-v_{1}^2}$

（3）斯涅耳定律

我们现在就来着手解决光在介质中折射的问题，在古希腊时，托勒玫和克莱门德曾经研究过光的折射，托勒玫把空气中若干个不同的角同与之一一对应的水中的角列成表，表如下。

空气中的角	水中的角	空气中的角	水中的角
10°	8°	50°	35°
20°	15.5°	60°	40.5°
30°	22.5°	70°	45.5°
40°	29°	80°	50°

我们想要寻找出隐藏在这些角度中的奥秘，1621年荷兰数学家斯涅耳找到了一个函数关系来表征两个角之间的关系：如果用θi表示空气中的角，θr表示水中的角，那么 $\frac{sin\theta_{i}}{sin\theta_{r}}=n$ ,其中n是一个常数，对于水和空气来说n大约为1.33，我们将用这条定律预测的数据列表如下：

空气中的角	水中的角	空气中的角	水中的角
10°	7.5°	50°	35°
20°	15°	60°	40.5°
30°	22°	70°	45°
40°	29°	80°	48°

我们发现预测值与托勒玫的实验值非常接近，上述有关角度的关系式称为斯涅耳定律。

（4）费马原理

我们已经有了斯涅耳定律解释光的折射，但是我们并不满足，因为斯涅耳定律相当于一种经验定律，并不是我们想要的那种可以解释自然发展规律的最根本的东西，我们说一切自然学科，不光是物理学，都要经历从观测实验，到建立模型，到解释实验现象的过程，正如费曼所说的“科学真正的光荣在于我们能够找到一种思维方式，使得定律称为明显的”。我们已经有了希罗最短路径原理，并且我们坚信上帝是个懒惰的人，他总是计算好以最经济最省力的方式完成目标。既然希罗最短路径无法解释折射现象，那么我们不妨换一个角度，光有没有可能总是走时间最短的路径呢。这让我们想到之前计算过的胡不归问题。

我们可以将光比作书生，那么胡不归问题相当于光以九十度入射，在介质中折射，根据之前的结论我们有

$\frac{v_{2}}{v_{1}}=cos\alpha=sin（90°-\alpha）$

我们定义α的余角为折射角，那么 $\frac{v_{2}}{v_{1}}=\frac{sin（90°-\alpha）}{sin(90°)}=\frac{1}n$

的确有常数比的关系！但是如果我们要把光看做书生，那就说明光在不同介质中的速度不同，实验表明，光在不同介质中的速度的确不同，这样我们就可以放心大胆地推演我们的理论了！

我们用n来表征光在两个介质中的相对速度，n称为相对折射率，其中光在介质1，2中的传播速率为 $v_{1}=\frac{c}{n_{1}},v_{2}=\frac{c}{n_{2}}$

所以 $n=\frac{n_{2}}{n_{1}}$

真空的ni值为1，光的传播速率为c（真空中光速）

斯涅耳定律可以表述为 $n_{1}sin(\theta1)=n_{2}sin(\theta_{2})$ ,θ1和θ2分别为入射角和折射角，n1和n2叫做折射率。

用以解释折射定律的最短时间原理是由费马在1650年左右发现的，他可以表述成如下形式：光传播的路径是光程取极值的路径，其中光程定义为折射率与路程的乘积，其实就相当于是时间最短（由于折射率和速度成反比，所以折射率乘路程与时间成正比）。

我们再次来观察这个最短时间原理，我们说，世界上其实并没有上帝，自然选择的方式往往是经过很多次尝试过后最有利的方式，或者是发生概率最高的方式。科学家们曾观察到一个奇特的现象，火蚁在通过两种不同介质的表面上时会形成类似折射光线的图案，如图所示

火蚁在经过两种不同介质时走过的路径类似于折射光线

这是因为，火蚁在不同介质中的行走速度不同，而在各个火蚁走不同路径时，他们相当于起到了一个试错的作用，他们的身上会留下气味，显然，使得到达目的点的时间最短的路径气味最浓，从而聚集的蚂蚁最多。

这也给我们一种解释光的折射定律的方式，我们不妨将光看成一个个蚂蚁，他们在空间的各个角度入射，但是相比之下在光程最短的邻近位置光程都趋于不变，相位趋近相同，而在其他位置光都互相叠加，相位互相抵消，总光强所剩无几，所以光显示出的路径近似为折射定律显示的路径，这种想法与费曼的路径积分有相通的地方。

（5）力学原理证明折射定律

在3blue1brown的频道中他曾经介绍了一种利用最小势能原理证明折射定律的方法，在这里简单叙述一下。

由于大自然并不只是在光学层面寻求极小值，在能量方面，力学构造会趋于势能曲线的最低点，因此我们只要找到类似的构造形式，就能将光学问题转化为力学问题。

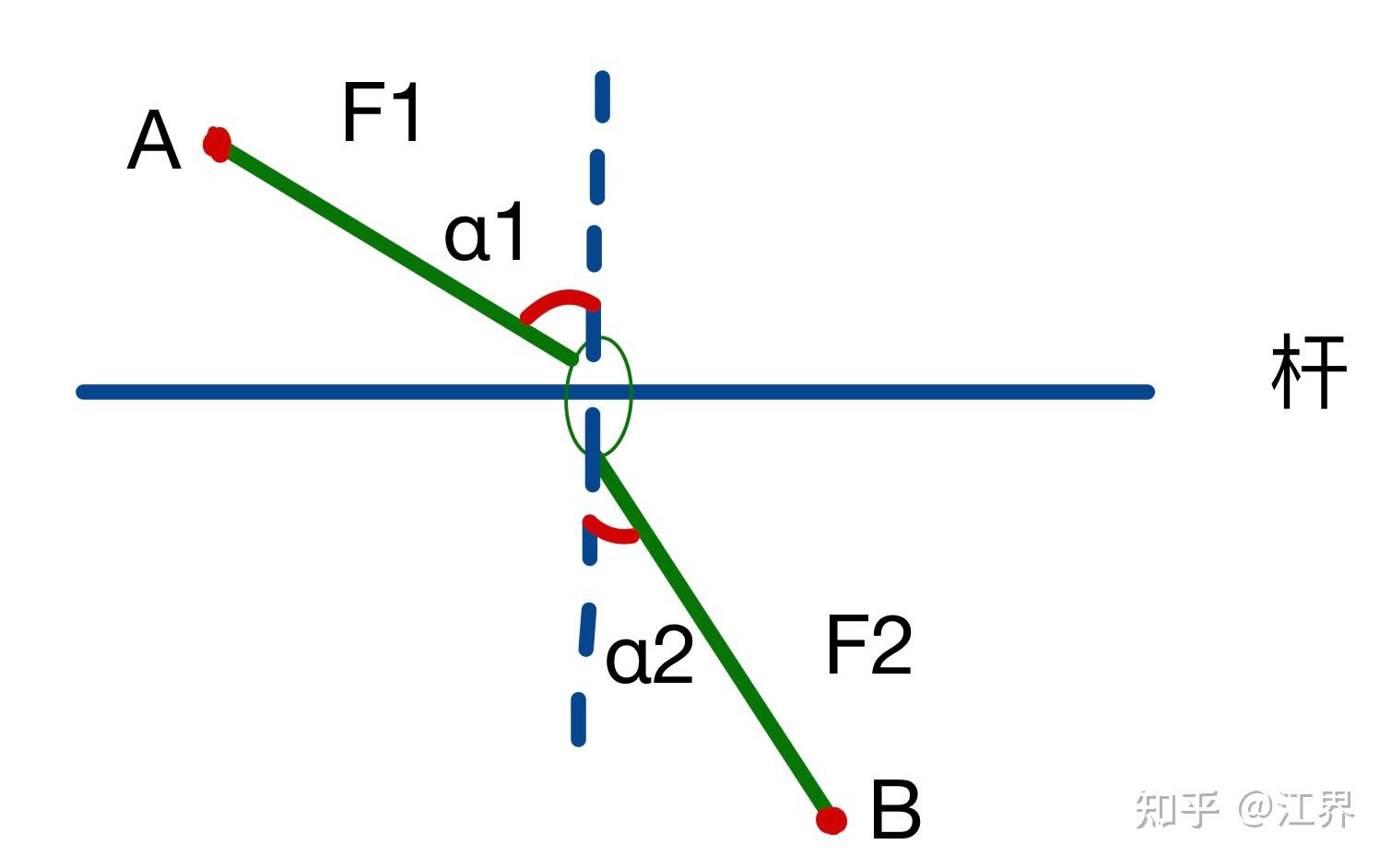
我们想象如图所示介质分界面为一根杆，有两根弹性绳连在套在杆的环上，我们将势能类比为光程，力就对应折射率 $（\frac{\partial U}{\partial L}=F,\frac{\partial{nl}}{\partial l}=n）$

力平衡态对应势能最小

由于力平衡态对应势能最小，平衡时我们有 $F_{1}sin\alpha_{1}=F_{2}sin\alpha_{2}$ ，于是我们就得到了折射定律：

$n_{1}sin\alpha_{1}=n_{2}sin\alpha_{2}$

（6）费马原理的应用：最速降线

如果你喜欢爬山，那么你可能会注意到我们通常登山的路线就是下大雨水流的路线（即水道）。但是如果你的朋友喜欢爬山，那你就危了（bushi）。最速降线指的是在重力作用下，粒子滑下所需的时间最短的路径。1638年，伽利略在荷兰莱顿出版的《关于两门新学科的对话》中提出了这个问题：

一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，沿着什么曲线滑下所需的时间最短？

当然伽利略本人也对这个问题做出了解答，只不过他的答案是错的，他认为这个曲线是圆弧。

1696年，著名的伯努利家族中的一员——约翰·伯努利对外公开征求最速降线问题的答案，这个约翰也是嚣张的很啊，他说：

“我，约翰·伯努利，向世界上最杰出的数学家喊话。对聪明人来说，没有什么比正确的、具有挑战性的问题更有吸引力的了，它的解决方案将赋予解答者名誉并作为永恒的纪念碑而存在。以帕斯卡、费马等人为榜样，我希望通过向我们这个时代最优秀的数学家提出一个考验他们方法和智力的问题，使他赢得整个科学界的崇敬。如果有人向我传达了所提出问题的解决方案，我将公开宣布他值得表扬”。

次年，各个科学大咖们都得到了正确答案（如牛顿、莱布尼兹、洛必达、约翰·伯努利、雅各布·伯努利等人）。

我们先来介绍约翰•伯努利的做法：

费马原理告诉我们，光总是走时间最短的路径，那么要求最速降线，我们何不让光他老人家亲自走一走呢？约翰·伯努利的做法就是，利用费马原理，将质点的运动等效为光的运动，用质点在某一点的速度表征光的折射率。

由于能量守恒，质点的速度仅与高度有关，于是我们将空间分成一层又一层的小份，每一份都有自己的折射率ni，如图所示

我们可以根据折射定律列出光线方程

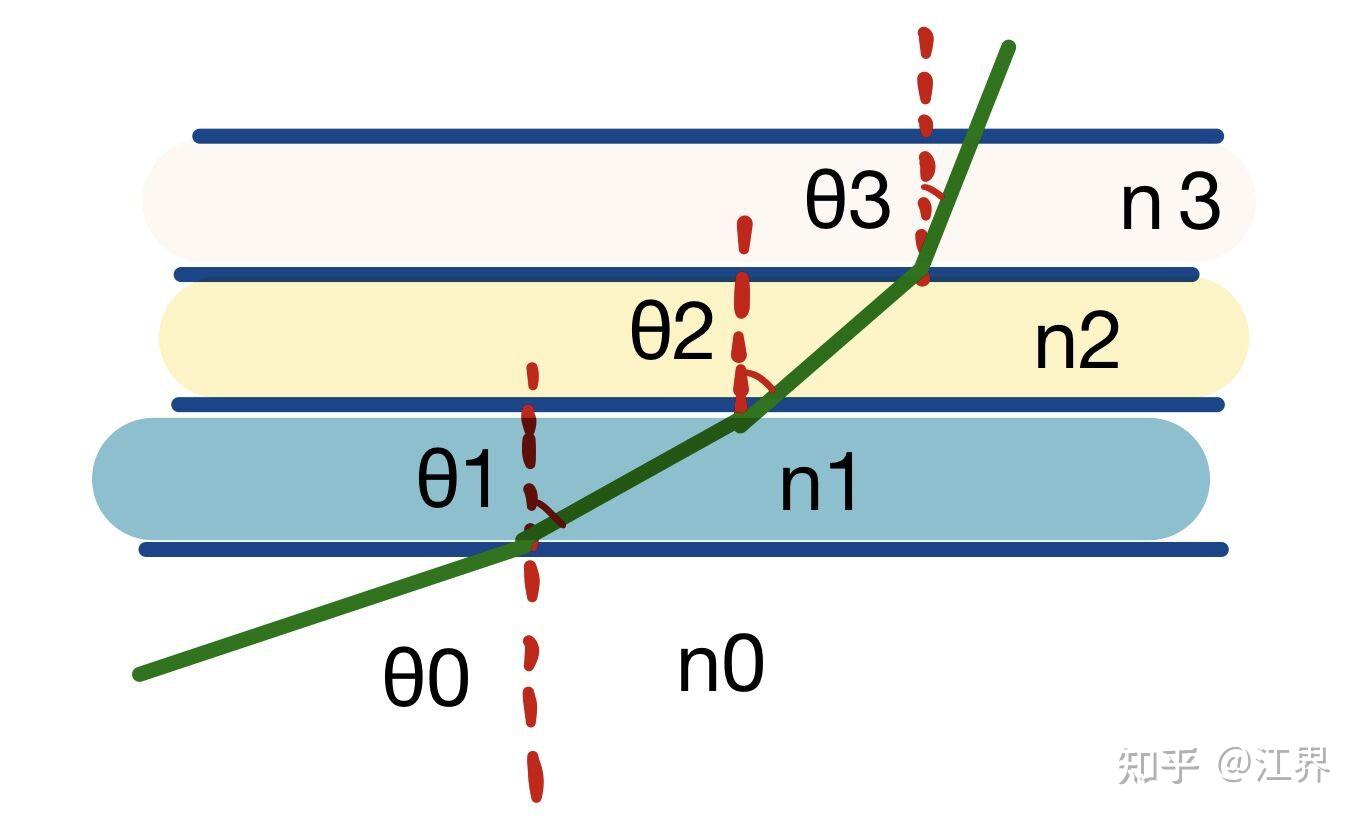
由斯涅耳定律，我们有 $n_{0}sin\theta_{0}=n_{1}sin\theta_{1}=n_{2}sin\theta_{2}=....n_{i}sin\theta{i}$ ，我们将离散的分层连续化,将微元变成微分

$sin\theta=\frac{dx}{ds}=\sqrt{\frac{1}{1+(\frac{dy}{dx})^2}}$ ，带入斯涅耳公式有

$n_{0}sin\theta_{0}=n(y)ain\theta(y)$

$(\frac{dy}{dx})^2=\frac{n^2(y)}{n_{0}^2sin^2\theta_{0}}-1$

于是我们得到

$\frac{dy}{dx}=\sqrt{\frac{n^2(y)}{n_{0}^2sin^2\theta_{0}}-1}$

$\frac{d\frac{dy}{dx}}{dx}=\frac{d\frac{dy}{dx}}{dy}·\frac{dy}{dx}=\frac{d^2y}{dx^2}=\frac{1}{2n_{0}^2sin^2\theta_{0}}\frac{d(n^2)}{dy}$

这就是光线方程

我们现在来着手解决最速降线的问题：建立如图所示坐标系

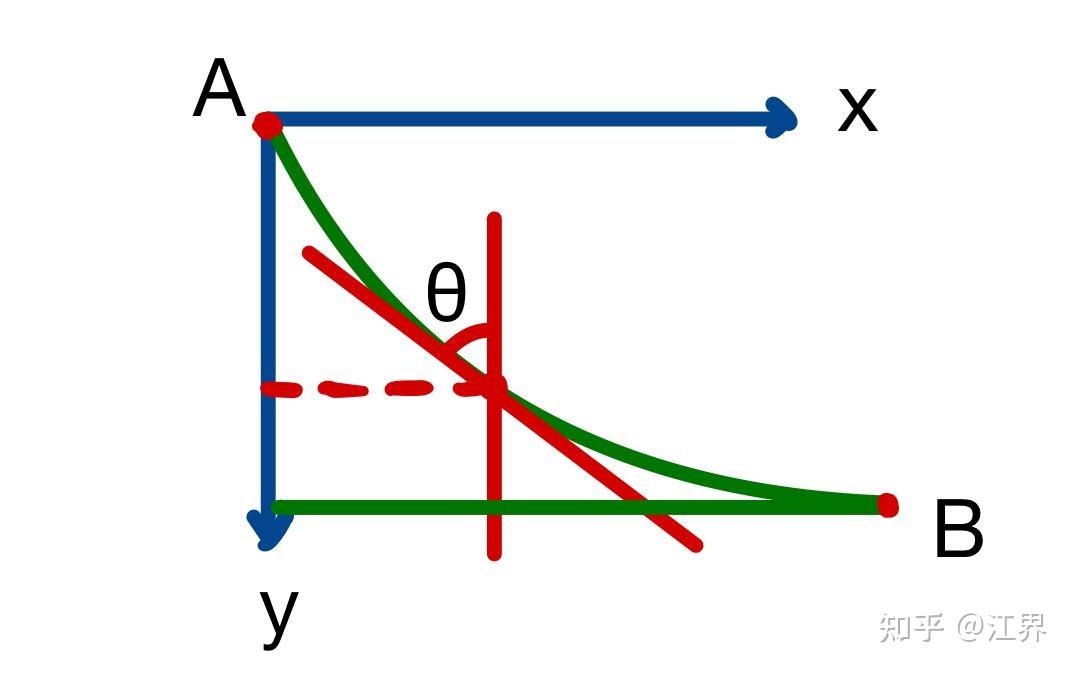
质点由A到B的运动可以类比为光的运动，质点每一y处的速度表征折射率。我们可以根据能量守恒求出质点速度：

$\frac{1}{2}mv^2=mgy \Rightarrow v=\sqrt{2gy}$

我们知道切线斜率代表了曲线的导数

即 $cot\theta=\frac{dy}{dx}$ 如果用y'表示y关于x的导数，那么sinθ为

$sin\theta=\frac{1}{\sqrt{y'^2+1}}$

由于速度表征了折射率，且速度和n成反比，我们假设nsinθ为一常量C

$\frac{sin\theta}{v}=C=\frac{\frac{1}{\sqrt{y'^2+1}}}{\sqrt{2gy}}$

$C\sqrt{2gy}\sqrt{y'^2+1}=1 \Rightarrow y(1+y'^2)=K$

注意这里换了个常数，但是无伤大雅，毕竟都是常量。

$y=\frac{K}{1+tan^2\theta}=Kcos^2\theta=Ksin^2(90°-\theta)$ 我们记90°-θ为θ'

$y=\frac{K}{2}(2sin^2\theta')=\frac{K}{2}(1-cos2\theta')$

设 $\theta'=\frac{1}{2}t$

所以 $y(t)=\frac{K}{2}(1-cost)$

接下来我们要解x（t）的参数方程

$y(1+y'^2)=K \Rightarrow \frac{dy}{dx}=\sqrt{\frac{K}{y}-1}$

$dx=\frac{dy}{\sqrt{\frac{K}{y}-1}}=dy\sqrt{\frac{y}{K-y}}$

我们将y（t）的表达式代入上式可以得到

$dx=\sqrt{\frac{\frac{K}{2}(1-cost)}{K-\frac{K}{2}+\frac{k}{2}cost}}=\sqrt{\frac{1-cost}{1+cost}}\frac{K}{2}sintdt=\frac{K}{2}(1-cost)dt$

积分不难得到 $x=\frac{K}{2}(t-sint)$

于是我们得到了最速降线关于t的参数方程

$\begin{cases} x=\alpha(t-sint)\\ y=\alpha(1-cost)\\ \end{cases}$

观察到x和y项中都有转动函数sint，cost，并且x中有直线运动函数t，所以我们可以将最速降线看成是一个纯滚动的轮子上的一点走过的路径，如下图所示

参量t如图所示，式子中的α就是轮子的半径

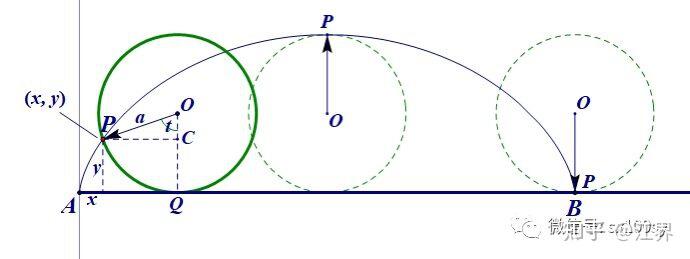
由于最速降线可以由这种方式得到，所以我们也称它为旋轮线或摆线。

（7）费马原理的应用：等光程法

“光总是走光程最短的路径”，费马原理只有这短短一句话，但就是这句话，将自然之美体现的淋漓尽致，现在我们来看看这句话告诉了我们什么：

1.光的路径有这样的性质：光程最短。

2.如果光沿着某条路径满足光程最短，从接收端发射的光从反方向沿该路径到达发出端也必然满足光程最短，即光路可逆。

3.多束光从同一点源出发经过某光学仪器，如果同时汇聚到一点或汇聚到无穷远处，那么该光学仪器需要使所有点源发出的光的光程相等，即等光程性。

下面我们来具体看一看等光程性是如何应用的：

例1.旋转抛物镜

试证明：从抛物面焦点发出的光线经反射后为平行光。

抛物线一点到焦点的距离与到准线距离相等

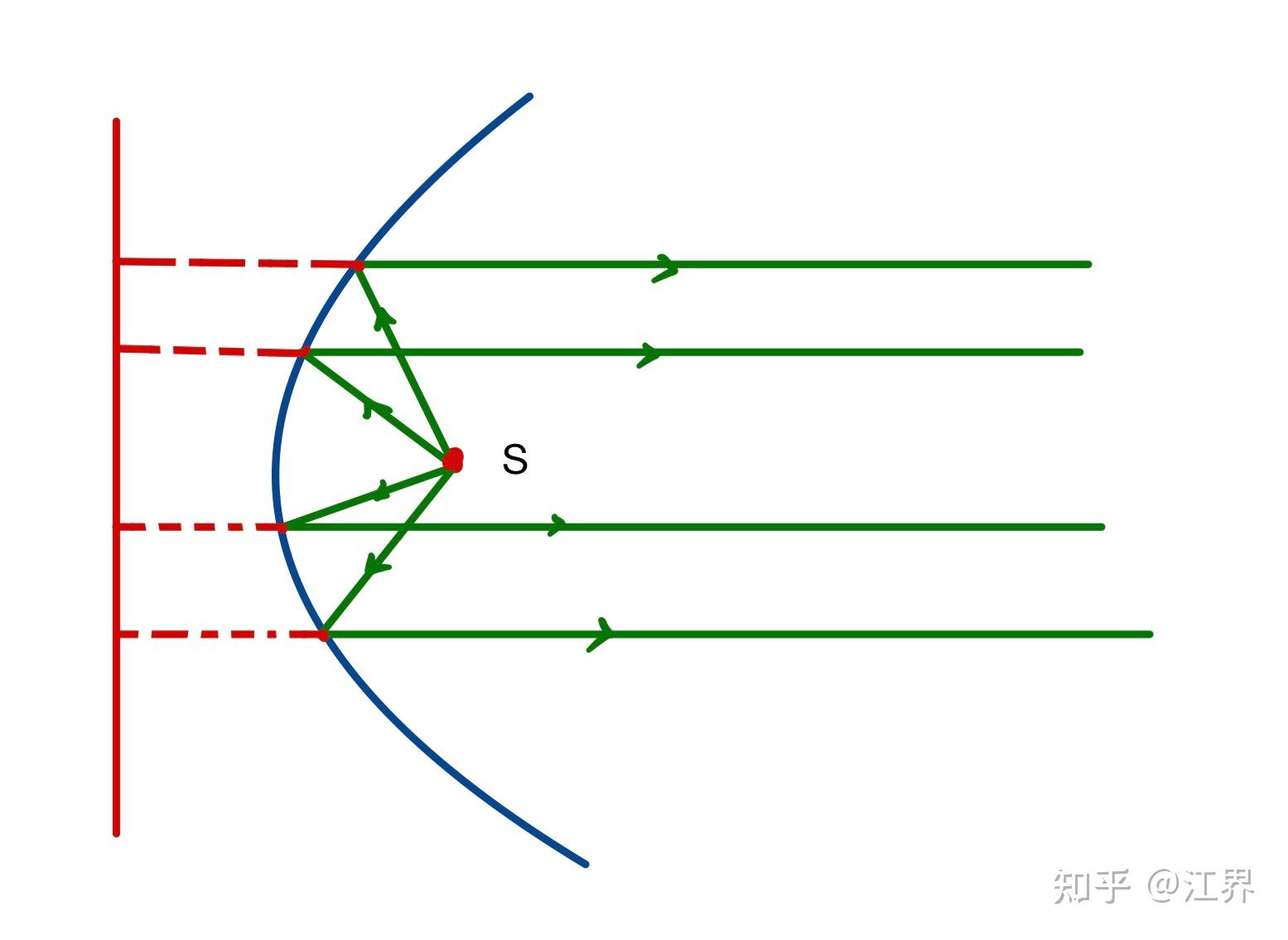
如图所示，根据抛物线的定义我们可以知道，抛物线上一点到焦点的距离与到准线的距离相同，于是我们可以画出准线，那么从S点发出的光的光程等于从准线上一点平行发出的光的光程，由于这些光程都相等，所以满足等光程性，该光线即为真实光路。

例2.椭球镜面

我们想要设计这样一种镜子，使得所有从P点入射的光都汇聚在P'点，试证明：椭球镜面满足这样的性质，且P、P'点在其焦点上。

椭球上的点到P和P'的距离之和为一常量

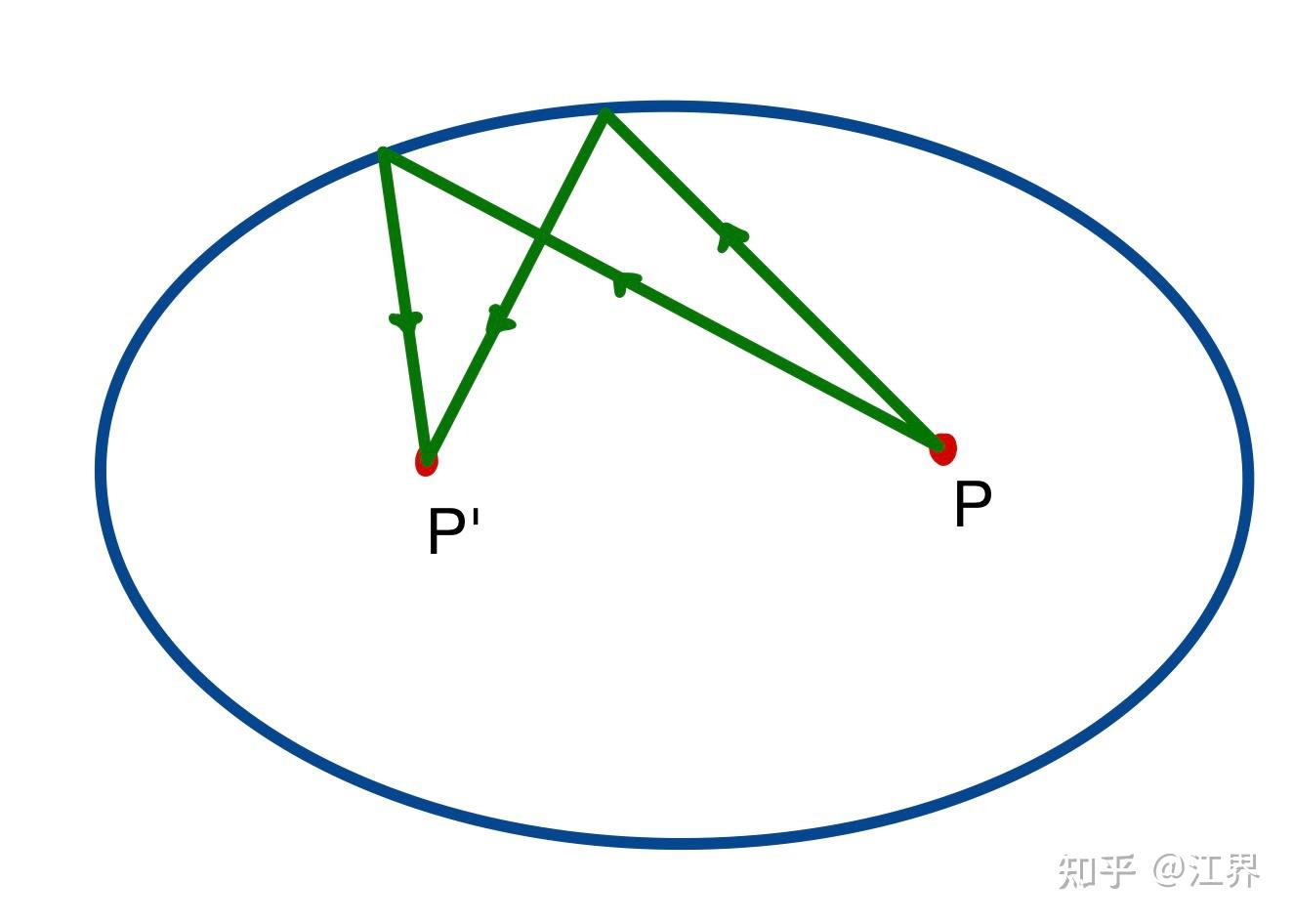
由于要求所有从P入射的光线都汇聚到P'点，那么我们假设A点为镜面上一点，那么必然满足等光程性，即PA+AP'为一定值，根据椭球的定义得证。

例3.引力透镜【39届复赛延期卷】

根据广义相对论，当光线经过某大质量球对称天体附近时，会向天体方向弯曲一个很小的角度ε，ε称为偏折角，即出射光与入射光的夹角，已知 $\varepsilon=\frac{R}{r}$ ，其中常数 $R=\frac{4GM}{c^2}$ ,r为光线与天体中心的最近距离，G为万有引力常数，M为天体质量，c为真空中光速。物理常数和单位： $c=3\times10^8m\cdot s^{-1}$ , $G=6.67×10^{-11}N\cdot m^2\cdot kg^{-2}$ ，1秒差距 $=3.09×10^{16}m$ ，1毫弧秒 $=10^{-3}×\frac{2\pi}{360\times3600}rad$ 。

（1）如图所示，当发光背景天体、大质量球对称天体以及望远镜恰好处在同一条直线上时，望远镜会观测到爱因斯坦环这一引力透镜现象。已知一背景天体发出的光线通过某紧邻白矮星附近时，形成的爱因斯坦环相对于望远镜的角半径 $\theta_{E}=31.53$ 毫弧秒，近邻白矮星到望远镜的距离为 $d_{L}=5.52$ 秒差距，背景天体到望远镜的距离为 $d_{s}=2\times10^3$ 秒差距。求该近邻白矮星的质量M。

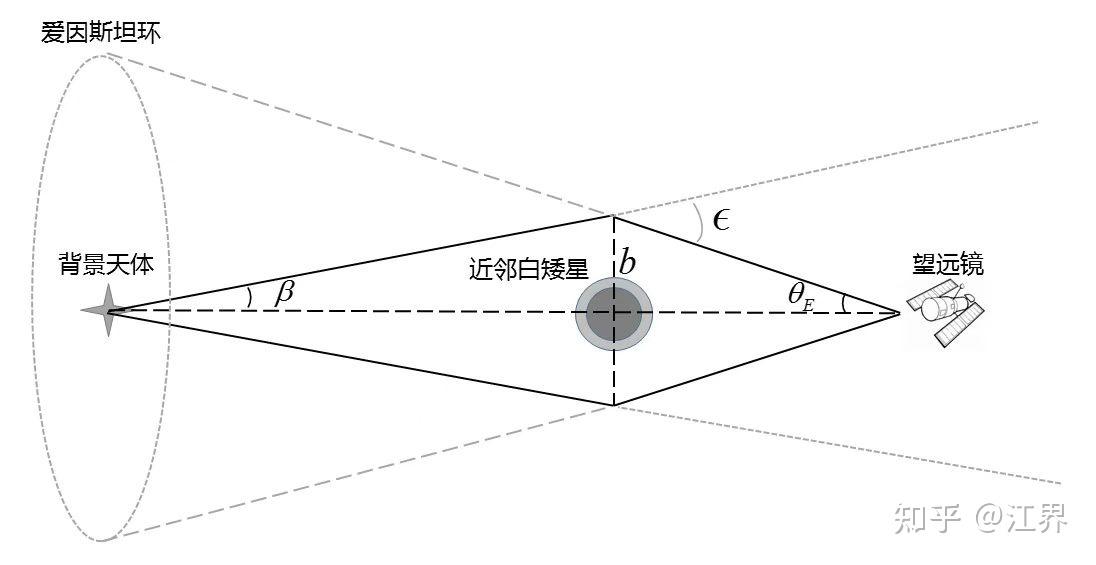
在图中标记各量如下：偏折角ε，偏折前的光线与三者连线的夹角为β，光线离近邻白矮星中心的最近距离近似为b（由于β很小，所以直角边和斜边近似相等）。另设背景天体到望远镜的距离为 $d_{s}$ ，近邻白矮星到望远镜的距离为 $d_{L}$ ，背景天体到近邻白矮星的距离为 $d_{Ls}$ 。

由几何关系和题目中的公式有

$\varepsilon=\theta_{E}+\beta=\frac{4GM}{c^2b}$

其中 $\theta_{E}\approx tan\theta_{E}=\frac{b}{d_{L}}$

$\beta\approx tan\beta=\frac{b}{d_{Ls}}$

所以我们得到 $\frac{b}{d_{Ls}}+\frac{b}{d_{L}}=\frac{4GM}{c^2b}$

解得 $b=(\frac{4GM}{c^2}\frac{d_{Ls}d_{L}}{d_{L}+d_{Ls}})^{\frac{1}{2}}=(\frac{4GM}{c^2}\frac{d_{Ls}d_{L}}{d_{s}})^{\frac{1}{2}}$

爱因斯坦环相对于观察者的角半径

$\theta_{E}=\frac{b}{d_{L}}=(\frac{4GM}{c^2}\frac{d_{Ls}}{d_{L}d_{s}})^{\frac{1}{2}}=(\frac{4GM}{c^2}\frac{d_{s}-d_{L}}{d_{L}d_{s}})^{\frac{1}{2}}$

近邻白矮星的质量为

$M=\frac{c^2}{4G}\frac{d_{L}d_{s}\theta_{E}^2}{d_{s}-d_{L}}=\frac{c^2}{4G}\frac{d_{L}\theta_{E}^2}{1-\frac{d_{s}}{d_{L}}}=1.34\times10^{30}kg$

（2）引力透镜现象可以用一个轴对称光学透镜来模拟演示。透镜的横截面如图2b所示，x轴为旋转对称轴，透镜入射面在 $0\leq r＜r_{0}$ 的区域不透光，出射面垂直于x轴。假设光线平行于x轴入射，入射光与x轴距离为r，偏折角 $\varepsilon=\frac{R}{r}$ 。已知光学透镜的折射率为 $n_{0}(n_{0}＞1)$ ,空气折射率为1，偏折角ε可视为小角度。求透镜入射面在 $r\geq r_{0}$ 区域内的表达式x（r）。用r、n0、R和r0表示。

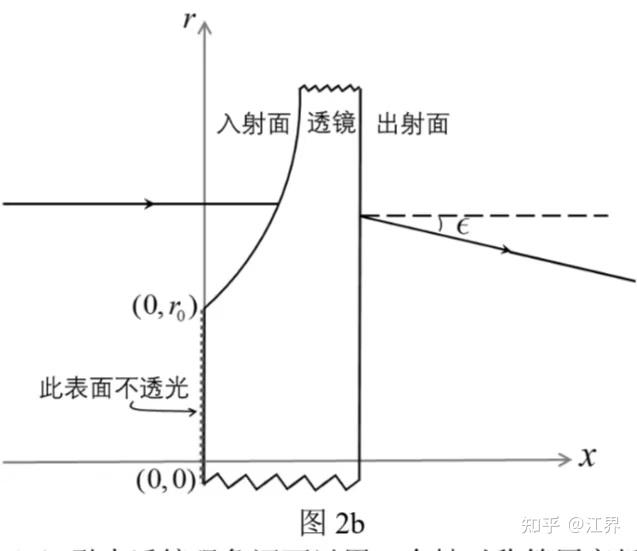
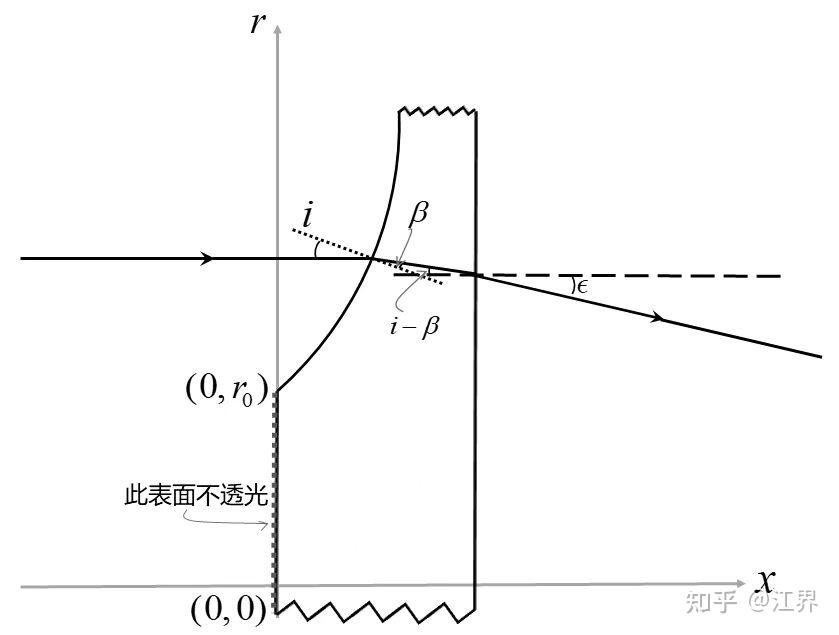
作出入射光线在透镜前表面的法线，入射角为i，折射角为β，根据折射定律有

$sini=n_{0}sin\beta$

作出光线在透镜后表面的法线，根据折射定律有

$n_{0}sin(i-\beta)=sin\varepsilon$

由于角度皆为小角，我们有

$n_{0}(i-\beta)\approx \varepsilon=\frac{R}{r}$

$\beta=i-\frac{R}{n_{0}}\cdot\frac{1}{r}$

代入到前面的式子中我们有

$sini=n_{0}sin(i-\frac{R}{n_{0}}\cdot\frac{1}{r})$

$sini=n_{0}[sinicos(\frac{R}{n_{0}r})-cosisin(\frac{R}{n_{0}r})]\approx n_{0}[sini-(\frac{R}{n_{0}r})cosi]$

$(n_{0}-1)sini=(\frac{R}{n_{0}r}cosi)$

$\frac{dx}{dr}=tani=sini=\frac{R}{n_{0}(n_{0}-1)r}$

积分可得 $x(r)=\frac{R}{n_{0}(n_{0}-1)}ln\frac{r}{r_{0}}$ 、

（3）引力透镜现象还可以用一个轴对称等厚变折射率透镜模拟演示。透镜的横截面如图2c所示，x轴为旋转对称轴，透镜厚度为D，透镜折射率为 $n（r）＞1$ 。假设光线垂直入射，入射光与x轴距离为r，忽略光线在透镜内的偏折，光线在透镜出射面的偏折角仍满足 $\varepsilon=\frac{R}{r}$ ，偏折角ε可视为小角度。已知 $n(r_{1})=n_{1}$ ，且 $r＜r_{1}$ 区域不透光。求透镜折射率在 $r\geq r_{1}$ 区域的表达式n（r），用r、n1、R、r1、D表示。

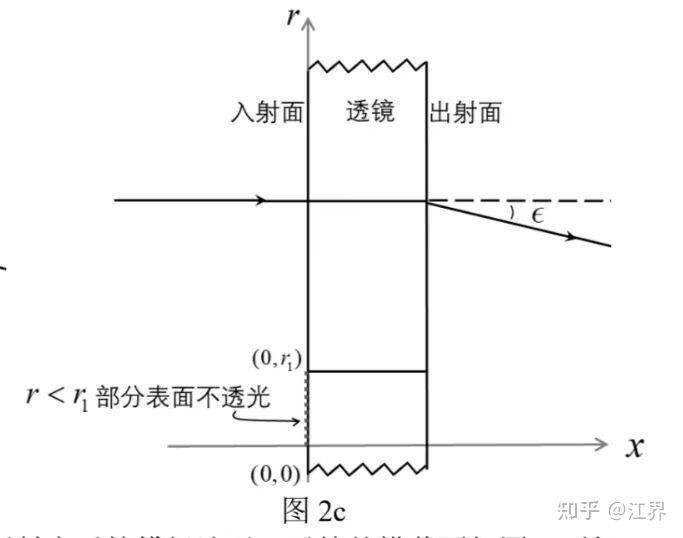
由于等光程性，我们考察两束平行入射，相距dr的光

$D(n(r+dr)-n(r))=-dr\varepsilon$

$D\frac{dn}{dr}=-\frac{R}{r}$

$\int_{0}^{n}dn=-\frac{R}{D}ln\frac{r}{r_{1}}$

$n=n_{1}-\frac{R}{D}ln\frac{r}{r_{1}}$

（二）莫培督最小作用量原理（Maupertuis' principle of least action）

（1）自然普遍的作用量

在费马提出最短时间原理后，十八世纪中叶，法国数学家莫培督（Pierre Louis de Maupertuis）重新研究了与自然作用有关的问题。物理学家们始终都有着一股信念，即我们可以用一个统一的规律去描述不同领域的物理现象，比如说，能量守恒、动量守恒以及角动量守恒，我们想要普遍性的东西，尤其是在有关自然本质的方面。费马原理的优美之处在于它用寥寥几句将上帝的面孔展现在我们面前，让人觉得似乎光就是自然生命的象征，光似乎就是自然的吐息。莫培督认为自然界中的最小量不应当只是光学中所消耗的时间，应当既满足光学中的费马原理，又对应牛顿力学的原理，这样的量才是自然普遍的。

1744年4月15日，在莫培督提交法兰西科学院题为《论各种似乎不协调自然定律间的一致性》的文章中，他写道：

自然在产生其效果时，总是选择最简单的手段......它所选取的途径是作用量的值最小的那个。

1746年，莫培督在《从形而上学原理推导运动和静止定律》中进一步写道：

这就是最小作用量原理，上帝的一个如此明智且有价值的原则，是所有自然现象所固有的......当自然界的一个变化发生时，这个变化所需要的作用量的值是所有可能中最小的那个，作用量的值是物质质量、速度和移动距离的乘积。

物质质量、速度和移动距离的乘积最小,这就叫做莫培督最小作用量原理。

（2）势场与莫培督原理

在“力学原理证明折射定律”中，我们提到势能与光程是等效的，我们想要找到一个满足牛顿力学的作用量，不妨建构一个类似于折射界面的力学体系，我们用不同的势场来实现这种等效。

如图所示，考虑图中光滑平面，它被直线 $x=x_{1}$ 分为两个区域，质量为m的质点在①区域中势能为0，在②区域中势能 $V=V_{0}$ ，该质点从原点O以 $\theta_{1}$ 的角度入射，速度为 $v_{1}$ ，在②中沿与x轴夹角为 $\theta_{2}$ 的直线运动至点P，到达点P时的速度为 $v_{2}$

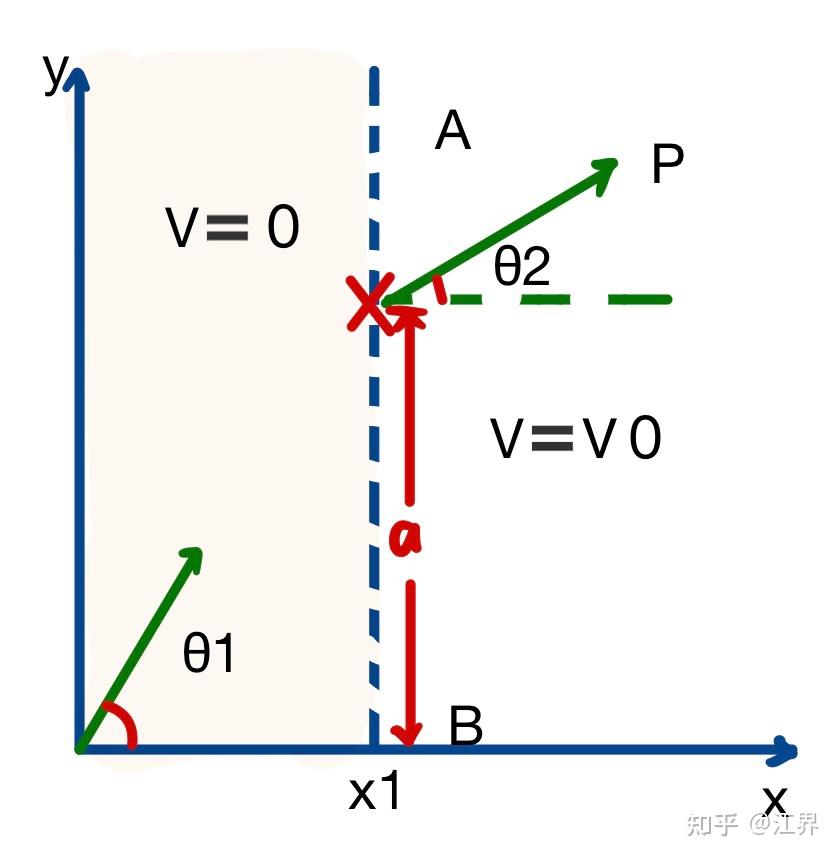
我们来寻找在这个过程中的不变量，而这个不变量就是相应的作用量的导数（由于作用量取极值，故导数为0）。

由能量守恒有 $\frac{1}{2}mv_{1}^2=\frac{1}{2}mv_{2}^2+V_{0}$

$v_{2}=\sqrt{{v_{1}^2}-\frac{2}{m}V_{0}}$

由于 $F=\frac{\partial V}{\partial x}$ 那么y方向由于势能不变，受力为0

所以可列y方向动量守恒有

$mv_{1}sin\theta_{1}=mv_{2}sin\theta_{2}$

设O点坐标为 $(0,0)$ ，P点坐标为 $(x_{0},y_{0})$ ，交界点坐标 $(x_{1},\alpha)$

可得 $\frac{mv_{1}\alpha}{\sqrt{x_{1}^2+\alpha^2}}-\frac{mv_{2}(y_{0}-\alpha)}{\sqrt{(x_{1}-x_{0})^2+(y_{0}-\alpha)^2}}=0$

所以作用量应该正比于 $\int_{}^{}m(\frac{v_{1}\alpha}{\sqrt{x_{1}^2+\alpha^2}}-\frac{v_{2}(y_{0}-\alpha)}{\sqrt{(x_{1}-x_{0})^2+(y_{0}-\alpha)^2}})d\alpha=mv_{1}\sqrt{x_{1}^2+\alpha^2}+mv_{2}\sqrt{(x_{0}-x_{1})^2+(y_{0}-\alpha)^2}$

等等

根号下这俩东西是不是长得有点别致，

它们就是质点走过的路径！

所以我们得到了作用量应当为 $S_{r}=mvs$

其中m为质量，s为质点走过的路径。

引入 $A=m\int_{}^{}v(s)ds$

莫培督原理即为，质点运动的路径满足A 取极值。

（3）折射定律的“矛盾”

在上述力学系统的推导中，我们应用了动量守恒 $mv_{1}sin\theta_{1}=mv_{2}sin\theta_{2}$

vsin的结构似乎与折射定律十分相似，

诶，这回怎么是v和sin 成反比了？？？

事实上，笛卡尔就曾经用“反过来”的式子推导折射定律，究竟哪里出了问题。

我们在“用力学原理推导折射定律”中似乎得到了正确的答案，当时我们将势能与光程类比，将折射率与力类比，得到受力平衡，巧了，这个受力方程也是y方向的受力为0。

如果我们假设莫培督原理是对的，且动量守恒定律成立，那么就说明，光的动量应当是与速度成反比的。

这是怎么一回事。。。。。。

在“量子力学初生”中我们知道了光子的动量确实是与速度成反比的，详见原文。

（4）极值原理和物质的波动性

德布罗意在提出物质波的过程中，运用了几何光学的费马原理和经典力学中莫培督原理的类比，并受到爱因斯坦关于光的波粒二象性的启示，德布罗意在追忆发现物质波的过程时曾经说道：

突然间，我萌发了把光的波粒二象性推广到物质粒子，尤其是电子的想法，我不能给出确切的日子，但一定是在1923年夏天。我认识到，一方面，哈密顿在某种程度上指出了这点，因为它能适用于粒子，同时又表示一种几何光学；另一方面，在量子现象中得到的量子数很少在力学中被找到，但却常常出现在波动现象以及与波动运动有光的所有问题中，于是，我自信有一种与量子现象相联系的波。

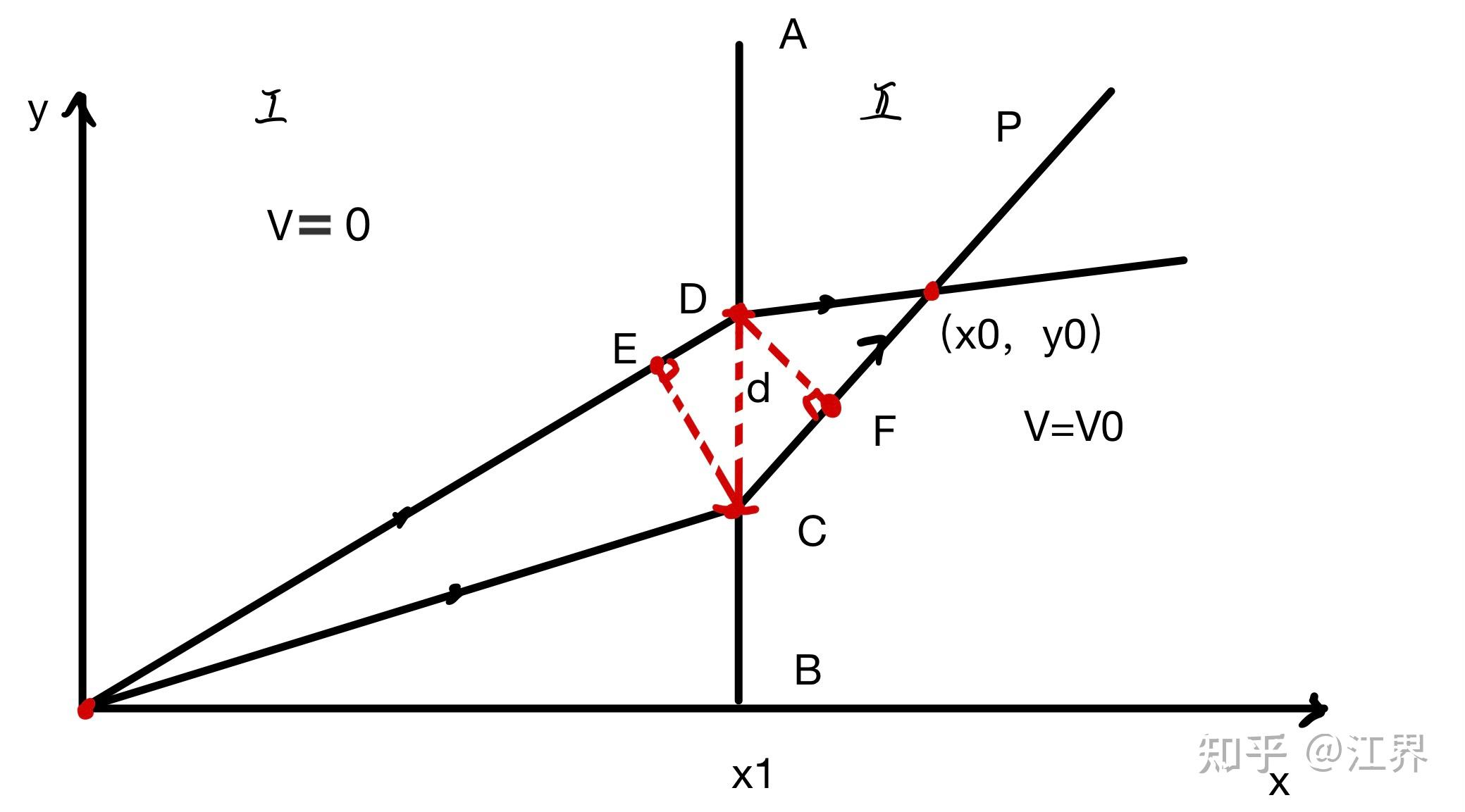
我们现在来讨论最小作用量原理和运动粒子的波动性之间的联系，如图所示，我们仍采用与势场部分相似的结构，以说明莫培督原理的普遍性，对此我们验证轨迹的思路为，先假定粒子由O点运动到P点的所有可能的轨迹，然后寻找依赖于德布罗意波干涉的轨迹。

首先我们想知道当粒子轨道之间差了一个距离时，他们的相位差异为多大。

我们已经知道（详见量子力学的初生）物质波的波长为 $\lambda=\frac{h}{mv}$

我们假设粒子在轨迹上移动了 $\Delta s$

那么德布罗意波的相位变化为 $\Delta \phi=\frac{2\pi\Delta s}{\lambda}=\frac{2\pi}{h}mv\Delta s=\frac{2\pi\Delta A}{h}$

这里的A就是我们之前定义的作用量。

接下来开始我们的证明：

如图，我们在边界AB上开一个小孔，宽度为d，其中 $d\ll x_{0}-x_{1}$

那么如果OCP为最小作用量所要求的轨道，那么物质波在轨道周围的相位应当接近，不然就会相消以至于宏观上与该轨道无缘，所以我们就要验证ODP和OCP轨道上粒子的相位差近似为0。

由于两条轨迹相位差主要出在DE边和CF边上

有了初步的推导，我们开始我们的证明:

$\Delta \phi=\frac{2\pi| \left| DE \right\|}{\lambda_{1}}-\frac{2\pi| \left| CF\right\|}{\lambda_{2}}\\ =\frac{2\pi}{h}(\frac{dsin\theta_{1}}{\lambda_{1}}-\frac{dsin\theta_{2}}{\lambda_{2}})\\ =\frac{2\pi md}{h}(v_{1}sin\theta_{1}-v_{2}sin\theta_{2}) \\ =0\\ \Rightarrow \Delta A=0$

得证，我们发现莫培督原理确实很好地将光学与力学结合在一起，于此我们似乎能窥探到波粒二象性的合理性，有关内容我们在哈密顿的光力类比中会说明。

（5）变分法

我们已经得到了莫培督原理，也知道了粒子所走的路径应当满足 $\Delta A=0$ ，但是问题来了：

我甚至连推导斜抛运动的能力都没有！

莫培督原理中的路径s实在是太复杂了，在实际问题中，这个s通常是一个不太友好的函数，有了理论却没有数学基础支持，真是件头疼的事。。。。。。

等等，条条大路通罗马，方法是人探索出来的，那么我们也可以试着探索一下解决的方式。

解决问题的第一步：理清问题的内容。

我们现在要求的是A积分的极值，它是一个对函数路径的积分，且满足极值条件告诉我们，在移动ds时，A几乎保持不变。所以我们想要的方法或者解决策略就是表示出一个积分 $\int_{s}^{}F(x_{1},x_{2}.....x_{n})dx_{m}$ 关于不同路径s的极值。

第二步：建立模型

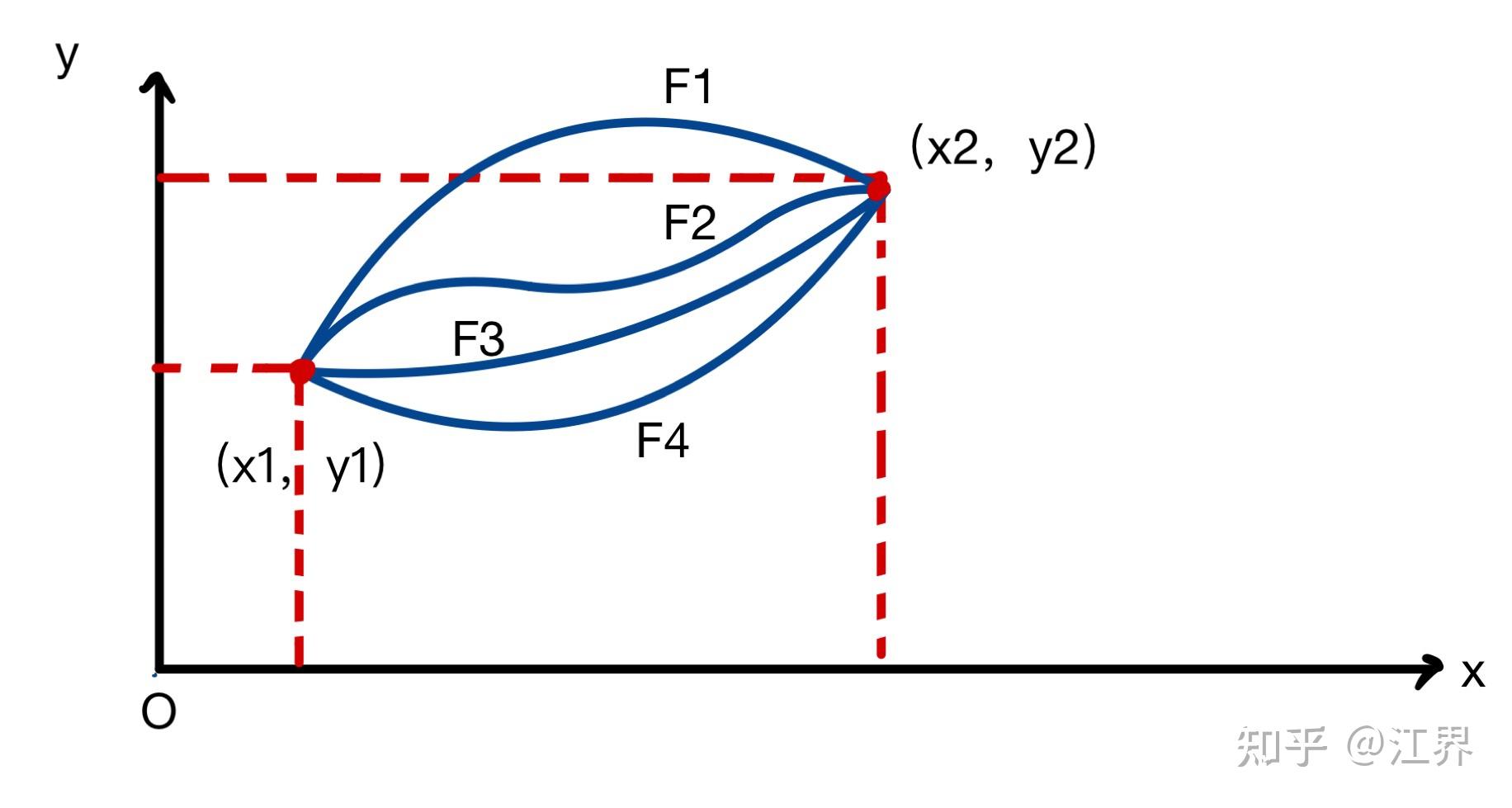
我们不妨取各种各样的路径，并用F表示此路径函数，并要求路径的起点和终点相同，那么路径的极值要求该积分在路径的微小扰动下保持不变，如图所示：

F1,F2,F3为粒子走过的不同种路径，但真正满足最小作用量原理的，是使得扰动附近的路径积分值不变的那条。

第三步：解决问题

我们设路径为u（x）那么，F是表示了不同路径的函数。为了简单起见，我们讨论二维路径情况，由于二维路径函数的所有信息可由三个参量，u，u的导数，x表示，所以 $F=F(u,u',x)$ 。

对于路径的小扰动，我们用εv(x)表示。

那么扰动后的路径设为 $w(x)=\varepsilon v(x)+u(x)$

根据我们之前起点和终点的假设，我们有 $v((x_{1},y_{1}))=v(a)=0\\v((x_{2},y_{2}))=v(b)=0$ a,b为引入的表示点的参量（纯粹是为了写的简单，没啥特殊含义，不用寻思了）。

我们记路径积分为I，I此时应当是ε的函数，即

$I(\varepsilon)=\int_{a}^{b}F(x,w,w')dx$

取极值要求 $\frac{dI}{d\varepsilon}=0$ ,即

$\frac{dI}{d\varepsilon}|_{\varepsilon=0}^{}=\frac{d}{d\varepsilon}\int_{a}^{b}F(x,w,w')dx\\=\int_{a}^{b}(\frac{\partial F}{\partial w}\frac{\partial w}{\partial \varepsilon}+\frac{\partial F}{\partial w'}\frac{\partial w'}{\partial \varepsilon})\\=0$ 当ε=0时 $\frac{\partial F}{\partial w}=\frac{\partial F}{\partial u}$

且有 $w'=u'(x)+\varepsilon v'(x)$

所以 $\frac{\partial w'}{\partial \varepsilon}=v',\frac{\partial F}{\partial w'}|_{\varepsilon=0}^{}=\frac{\partial F}{\partial u'}$ ，还有 $\frac{\partial F}{\partial w}=\frac{\partial F}{\partial u}$

改写原式可以得到

$\int_{a}^{b}(\frac{\partial F}{\partial u}v+\frac{\partial F}{\partial u'}v')dx=0$

我们想将v'换成v，这样我们可以根据被积分量等于0列出等式。

分部积分可以实现上述想法：

$\int_{a}^{b}\frac{\partial F}{\partial u'}v'dx=(\frac{\partial F}{\partial u'}v)|_{a}^{b}-\int_{a}^{b}\frac{d}{dx}(\frac{\partial F}{\partial u'})vdx$

由于起点和终点相同，所以

$\int_{a}^{b}\frac{\partial F}{\partial u'}v'dx=-\int_{a}^{b}\frac{d}{dx}(\frac{\partial F}{\partial u'})vdx$

代入原式我们可得

$\int_{a}^{b}（\frac{\partial F}{\partial u}-\frac{d}{dx}(\frac{\partial F}{\partial u'}))vdx=0\\ \Rightarrow \frac{\partial F}{\partial u}-\frac{d}{dx}(\frac{\partial F}{\partial u'})=0$ 上式称为欧拉-拉格朗日方程。

（6）最速降线的变分解法

我们可以用变分法求解最速降线问题（雅各布·伯努利解法）

由能量守恒，我们有 $v=\sqrt{2gy}$

且 $ds=vdt$

$dt=\frac{ds}{v}=\frac{\sqrt{1+y'^2}}{\sqrt{2gy}}dx$

所以时间可以表示为 $t=\int\frac{\sqrt{1+y'^2}}{\sqrt{2gy}}dx$

$F(x,y,y')=\frac{\sqrt{1+y'^2}}{\sqrt{y}}$

我们发现F不显含x

所以 $\frac{dF}{dx}=\frac{\partial F}{\partial y}\frac{\partial y}{\partial x}+\frac{\partial F}{\partial y'}\frac{\partial y'}{\partial x} =\frac{\partial F}{\partial y}y'+\frac{\partial F}{\partial y'}y''$ （F关于x的偏导为0）

$\frac{d}{dx}(y'\frac{\partial F}{\partial y'})=y''\frac{\partial F}{\partial y'}+y'\frac{d}{dx}(\frac{\partial F}{\partial y'})$

将上述两式相减可以得到

$y'(\frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})=0=\frac{d}{dx}(F-y'\frac{\partial F}{\partial y'})$

所以我们得到 $F-y'\frac{\partial F}{\partial y'}=C$

将我们式子中的F代入可得

$\frac{\sqrt{1+y'^2}}{\sqrt{y}}-y'\frac{y'}{\sqrt{y(1+y'^2)}}=C$

所以可以得到 $\frac{1}{\sqrt{y(1+y'^2)}}=C$

$\frac{dy}{dx}=\sqrt{\frac{k}{y}-1}$

这里的k为常数

积分可以得到

$x=(y-k)\sqrt{\frac{y}{k-y}}+k \cdot arctan(\sqrt{\frac{y}{k-y}})$

易验证 $\begin{cases} x=\frac{k}{2}(\theta-sin\theta)\\ y=\frac{k}{2}(1-cos\theta)\\\end{cases}$

为解

例4.求有摩擦质点的最速降线。

大家可以动脑想一想，对于有摩擦情况，我们如何求解。

不妨设摩擦系数为 $\mu$ ，那么根据受力分析我们可以得到 $m\frac{dv}{dt}=mgsin\theta-\mu mgcos\theta=mg\frac{dy}{ds}-\mu mg\frac{dx}{ds}=\frac{1}{2}m\frac{dv^2}{dx}$

所以我们有 $\frac{1}{2}dv^2=g(dy-\mu dx)\\ v= \sqrt{2g(y-\mu x)}\\ t=\frac{1}{\sqrt{2g}}\int\frac{\sqrt{1+y'^2}}{\sqrt{y-\mu x}}dx$

代入欧拉-拉格朗日方程我们得到

$(1+y'^2)(1+\mu y')+2(y-\mu x)y''=0\\ \frac{1+y'^2}{(1+\mu y')^2}=\frac{C}{y-\mu x}$

令 $y'=cot\frac{\theta}{2}$

则解得 $\begin{cases} x=\frac{k}{2}(\theta-sin\theta)+\mu(2-cos\theta)\\ y=\frac{k}{2}(1-cos\theta)+\mu(\theta+sin\theta)\\ \end{cases}$

例5.有心力场下的最速降线^[1]

关于平方反比引力作用下物体运动的研究已经十分深入，拥有质量m、角动量L ，以及能量E的物体在质量为M的中心天体吸引力下的轨迹为

$r=\frac{P}{1+ecos\theta}$ 其中

$\begin{cases}P=\frac{L^2}{GMm^2}\\e=\sqrt{1+\frac{2EL^2}{G^2M^2m^3}}\end{cases}$

但事实上这个路径并不是引力场下耗时最短的路径。以下我们假设飞船在运动过程中燃料只用以改变运动方向，运动速度的大小仅由势能影响。

如图，若在一势场V（r）的作用下，飞船从B（近心点）到A（远心点）的耗时最短的路径恰恰就是 $r=\frac{P}{1+ecos\theta}$

飞船的能量为E，在B点时，飞船速度为v0，求势场V（r）的表达式。

将飞船在势场中的运动等效成光在折射率为n（r）的介质中传播。由折射定律可得

$nrsin\phi=Const$

$tan\phi=\frac{rd\theta}{dr}=\frac{p}{ersin\theta}$

代入我们可以得到

$n(r)=A\sqrt{\frac{e^2sin^2\theta}{p^2}+\frac{1}{r^2}}=A\sqrt{\frac{e^2-1}{p^2}+\frac{2}{rp}}$

其中A为待定常数

我们利用折射率的定义 $n=\frac{c}{v}$

代入初始条件 $r=\frac{p}{1+e},v=v_{0}$

可以得到 $v（r）=\frac{c}{A\sqrt{\frac{e^2-1}{p^2}+\frac{2}{rp}}}=\frac{v_{0}(1+e)}{\sqrt{e^2-1+\frac{2p}{r}}}$

由能量守恒我们可以得到

$V(r)=E-\frac{mv_{0}^2(1+e)^2}{2(e^2-1+\frac{2p}{r})}$

（7）莫培督原理的验证

我们现在来看个例子，用以验证莫培督原理。

例6.斜抛运动

试用莫培督原理验证质点斜抛运动的轨迹。

首先我们写出作用量： $A=m\int_{}^{}v(x,y)ds=m\int_{}^{}v(x,y)\sqrt{1+y'(x)^2}dx$

如果仿照之前的论证，我们选择 $y(x)=y_{0}(x)+\varepsilon y_{1}(x)$

$\delta A(y_{0},y_{1})=\int_{}^{}\left[ \frac{v(x,y_{0})y_{0}'y_{1}'}{\sqrt{1+y_{0}'(x)^2}}+v_{y}(x,y_{0})y_{1}\sqrt{1+y_{0}'^2}\right]dx$

可得到拉格朗日方程形式：

$-\frac{d}{dx}\left[ \frac{v(x,y_{0})y_{0}'}{\sqrt{1+y_{0}'^2}}\right]+v_{y}(x,y_{0})\sqrt{1+y_{0}'^2}=0$

其中 $v_{y}=\frac{\partial v(x,y)}{\partial y}$

由能量守恒我们可得

$v=\sqrt{v_{0}^2-2gy}$

代入方程我们可得

$\frac{\sqrt{1+y'^2}(vy''+v'y')-vy'\frac{y'y''}{\sqrt{1+y'^2}}}{{1+y'^2}}=\frac{\partial v}{\partial y}\sqrt{1+y'^2}$

$v'=\frac{\partial v}{\partial y}y'$

由于 $vy''\sqrt{1+y'^2}-vy'\frac{y'y''}{\sqrt{1+y'^2}}=\frac{vy''}{\sqrt{1+y'^2}}$

且 $\frac{\partial v}{\partial y}=\frac{-g}{\sqrt{v_{0}^2-2gy}}$

代入原式可得

$\frac{\frac{vy''}{\sqrt{1+y'^2}}-\frac{y'^2g\sqrt{1+y'^2}}{v}}{1+y'^2}=-\frac{g}{v}\sqrt{1+y'^2}$

$\frac{{vy''}-\frac{y'^2g(1+y'^2)}{v}}{1+y'^2}=-\frac{g}{v}({1+y'^2)}$

为了方便起见，我们只做数值验证，不做具体推导。

正常情况下，斜抛运动方程应当为

$\begin{cases} x=v_{x0}t\\ y=v_{y0}t-\frac{1}{2}gt^2\\ \end{cases}$

从而得到y（x）

$y(x)=\frac{v_{y0}}{v_{x0}}x-\frac{1}{2}\frac{gx^2}{v_{x}^2}$

我们不妨设 $v_{y0}=4\\ v_{x0}=3\\ x=1$ 不难得到 $\begin{cases} y=\frac{7}{9}\\ y'=\frac{2}{9}\\ y''=-\frac{10}{9}\\ v=\frac{\sqrt{85}}{3}\\ \end{cases}$

代入验证等式是否成立

等式左侧为 $\frac{-\frac{10\sqrt{85}}{9\times3}-\frac{\frac{4\times10}{81}\times\frac{85}{81}}{\frac{\sqrt{85}}{3}}}{\frac{85}{81}}$

等式右侧为 $-\frac{30\times85}{81\sqrt{85}}$

两侧确实相等（自己动手算一下试试）。

我们不仅验证了我们式子的正确性，也验证了莫培督原理的正确性，即我们可以用

$\frac{\sqrt{1+y'^2}(vy''+v'y')-vy'\frac{y'y''}{\sqrt{1+y'^2}}}{{1+y'^2}}=\frac{\partial v}{\partial y}\sqrt{1+y'^2}$ 描绘有关质点轨道的所有信息，

但是在求解过程中，我们发现解方程，那是异常的麻烦，我们怎么将它变得简单一些呢，世界上只有莫培督的一个作用量吗，有没有更加优美的体系呢，带着这些问题，我们接着来看第三部分：拉格朗日力学。

（三）拉格朗日力学

（1）拉格朗日量与哈密顿原理

我们现在想要找到另一个函数f作为新的最小作用量，由欧拉方程，我们知道首先它需要有三个参量 $f(u,u',x)$

且满足 $\frac{\partial f}{\partial u}-\frac{d}{dx}(\frac{\partial f}{\partial u'})=0$

在篇一：相对性原理时我们知道，根据牛顿决定论，如果知道质点某时的位移和速度，我们就能预测出它的运动，也就是说，在经典力学中（x，v，t）是满足描述一个系统整体的独立参量。相似的还有（θ，ω，t）。

这些可以描述力学系统的独立参量都有着（坐标，速度，时间）的结构，所以我们给所有类似的独立参量起名，坐标项的叫做广义坐标（generalized coordinates），速度项的叫做广义速度（generalized velocity），时间项呢？时间就是时间，没有广义之分，当然你也可以定义广义时间，例如 $t'=ct$ 表示时间轴上的位移，定义上我们不做过多解释，因为东西还是那个东西，只不过换了个名字。在兵荒马乱的年代，我们只能看脸识人，谁也不知道对方叫什么，说不定人家有几十个名字呢，关键是要抓住定义的本质。

我们不妨将f的三个参量对应于描述力学系统的那组独立参量，我们将广义坐标记作 $q$ ,广义速度记作 $\dot{q}$ 。

（有的人可能会有疑问了，为什么不写成 $q'$ 呢？在物理学的语境中， $q'$ 常常是对位移求导，而 $\dot{q}$ 才是对时间求导。）

我们接着来考察f的具体形式。在相对性原理一篇中，我们提到过，伽利略构造满足时间平移不变性、空间平移不变性以及空间旋转不变性，见下：

时间平移不变意味着 $F(x,x',t)=F(x,x',t+s) \rightarrow F(x,x'）$ 即F中不显含t

空间平移不变即空间各点有着相同的性质，即F仅取决于两点间的相对坐标 $x_{i}-x_{j}$

匀速运动不变，意味着惯性系的方程只依赖于相对速度 $x_{i}'-x_{j}'$

空间旋转不变，意味着空间是各向同性的，即有 $F（Gx,Gx'）=GF(x,x')$

函数 $f$ 也有同样的性质，只不过这里的f针对的是单一质点，所以我们有

f中不显含t，不显含q，空间旋转不变意味着f只与 $\dot{q}$ 的大小有关，即 $f=f(\dot{q}^2)$

我们把它代入欧拉-拉格朗日方程，可以得到

$\frac{\partial f}{\partial q}-\frac{d}{dt}(\frac{\partial f}{\partial \dot{q}})=0$

对于漂浮在空间中不受外力的单一质点来说，上式意味着速度关于时间的导数为0，即质点做匀速直线运动。

如果对于多质点保守体系而言，f的空间平移不变性要变成，f与相对坐标有关。

观察单质点f的形式，v的平方，似乎与动能相关。而我们列出多质点系统的牛顿方程：

$F=-\frac{\partial V}{\partial q}\\=m\frac{d}{dt}(\dot{q})\\=\frac{d}{dt}(m\dot{q})\\=\frac{d}{dt}[\frac{\partial }{\partial \dot{q}}(\frac{1}{2}m\dot{q}^2)]\\ =\frac{d}{dt}\frac{\partial T}{\partial \dot{q}}$ 我们发现应当满足 $\frac{d}{dt}\frac{\partial T}{\partial \dot{q}}+\frac{\partial V}{\partial q}=0$