有哪些你想发明却已经被人发明了的东西？

初三时发现了一些暴虐中考压轴二次函数题的方法，开始还以为只有我知道而兴奋了好久

提前说明一下，因为我们那几年中考压轴题基本不看步骤只看答案，所以我们做题用的方法都比较自由，而当时我又正好自学到了导数，被迷得神魂颠倒，自然就想试试用导数做做这些压轴题

一种很常见的第一问题型是

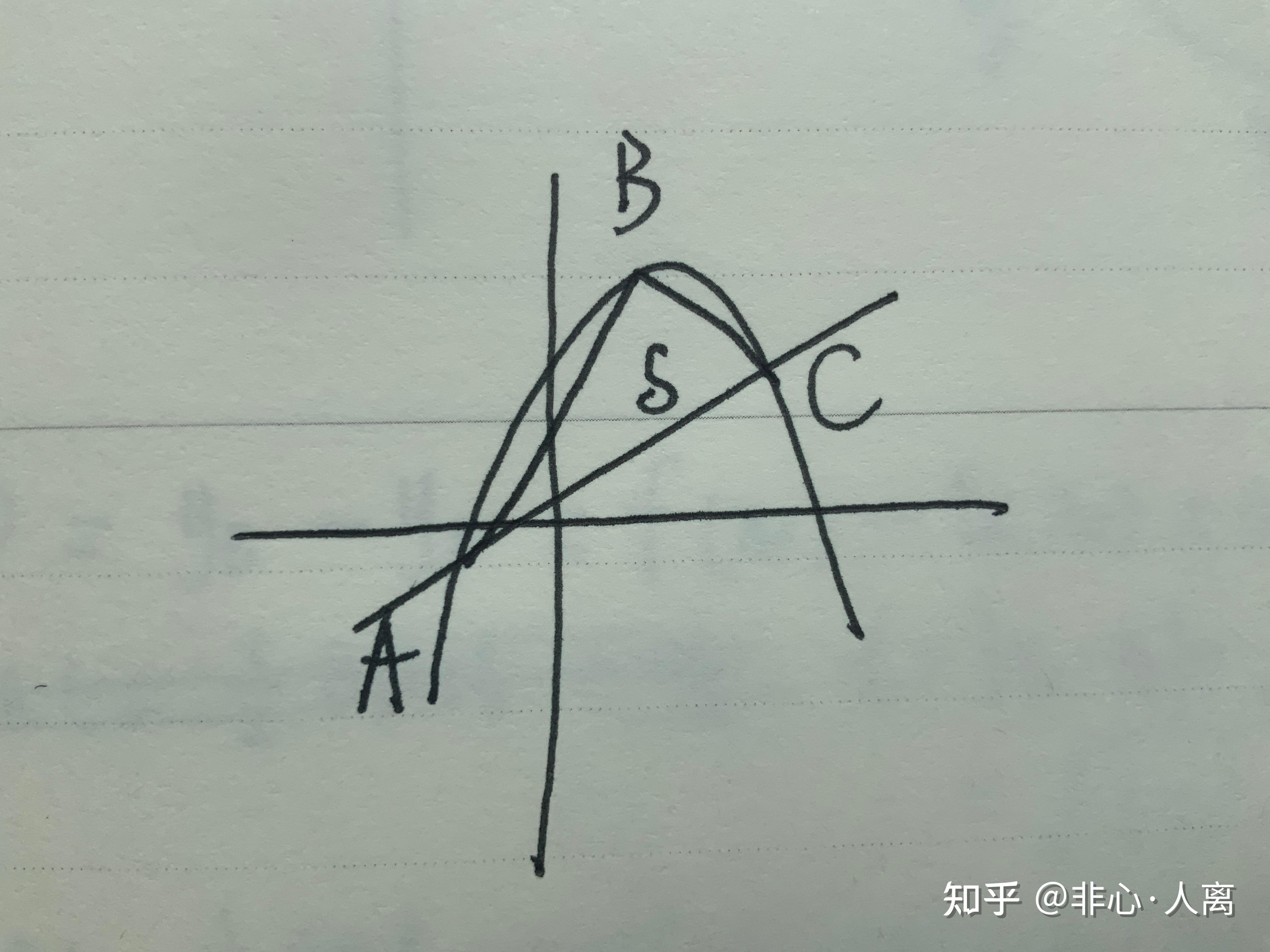
求b在哪里时三角形面积最大，虽然很简单可以硬算推出b在ac正中间时面积最大，但是当我用导数算的时候，过程比起硬算直接简洁了几个档次，把我狠狠惊艳到了

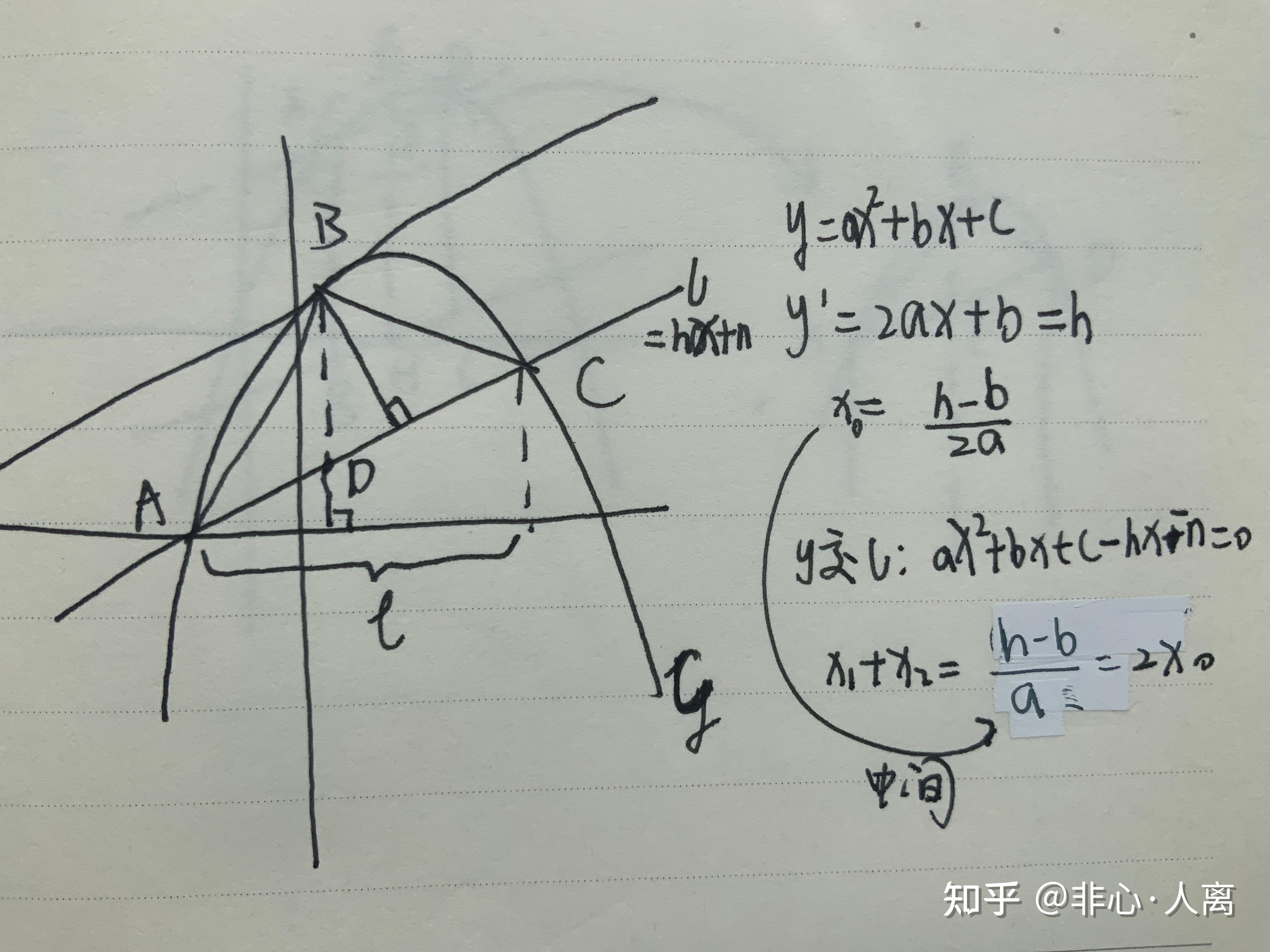
既然如此简洁，我索性就想算算三角形此时的面积，结果得出一个更惊人的结论！

这个面积公式竟然简洁得只与ac水平宽和二次函数的首相系数有关！有一次很难的模考压轴最后一题刚好就是算这个面积，用了这个公式直接比同学们提前20分钟结束战斗，让我好有成就感哈哈。

但更是让我直接高潮了几天的是下面这个题的出现

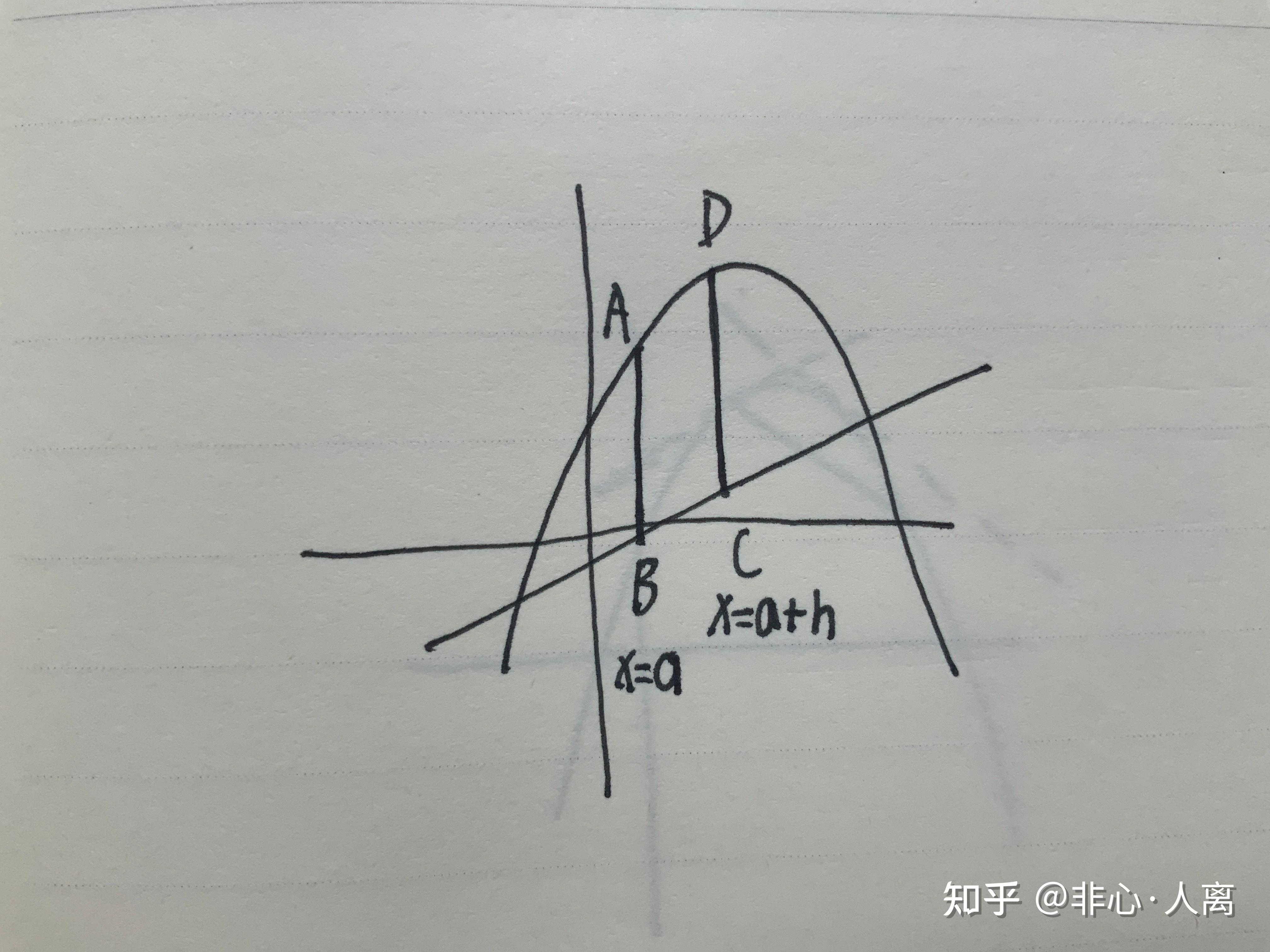
这次模考又变了个形，是求AB和CD两条相距h的垂线加起来最长是什么时候。虽然年级上还是有一些人用硬算算了出来，我也一开始是这么想的，但是当我试图去简化问题时，一条新的路出现了，并亮瞎了我的狗眼

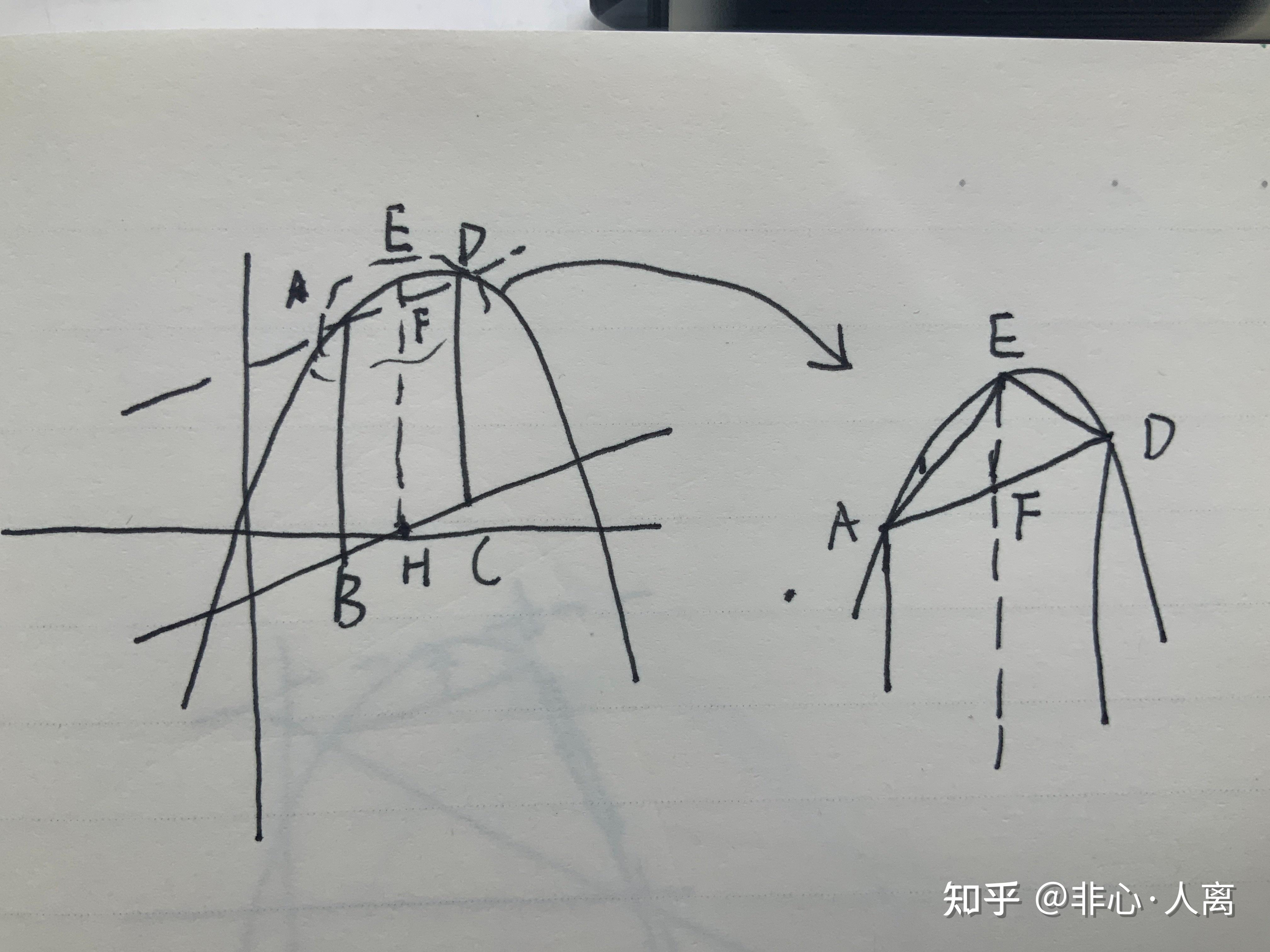
一开始我想能不能把两条线这个条件转化到一条线上面去，看着AB+CD这个式子，我突然想到了连接AD，那么我们就得到了一个梯形，而梯形的中位线恰恰是（上底+下底）/2，所以就能转换到讨论中位线HF上了，而一个很自然的想法就是延长HF到E去交与抛物线，这时候HF的长度就能转换为HE-FE了。

这时候美丽的一幕就来了，正是因为是中位线F处于AD正中间，三角形AED的面积是处于最大状态，对应的面积公式刚好是我不久前才算出来的(ah^3)/8，而AD水平宽=h根据条件是不变的，这不正意味着这个三角形的面积也是一个定值吗！而与此同时又因为三角形面积=铅锤高EF·水平宽/2，我们行云流水般得到了EF为定值这一个条件！（这些思路看着多其实在脑子里是一闪而过，顿时豁然开朗的感觉）那么就意味着当EH最长时，问题便解决了，而这个不正是最简单原始的第一种题型吗！

通过一堆操作硬是把最难算的题做成了最简单的题，别提当时有多幸福了。

当然这个可能扯远了，也辛苦各位读到这里的读者，但是那种一环扣一环，一个从问题中诞生的问题又解决了另一个问题的感觉实在是太棒了，希望你们也可以感受到。

导数法还有很多应用，在我的压轴题作业中百战百胜，po几个用导数法做要简单且快一倍的题（可能会误导一些人，但现在的大部分中考都不能超纲的，大家就看个乐，没事自己也可以研究着玩，不要用到考试就行，重点是主动知识迁移）

哈哈这个第二问简直是为我量身定制，还故意求立方根怕不是出题人也知道这个三角形面积公式，最后一问求直角三角形两边可以转化为切线再算，非常舒适

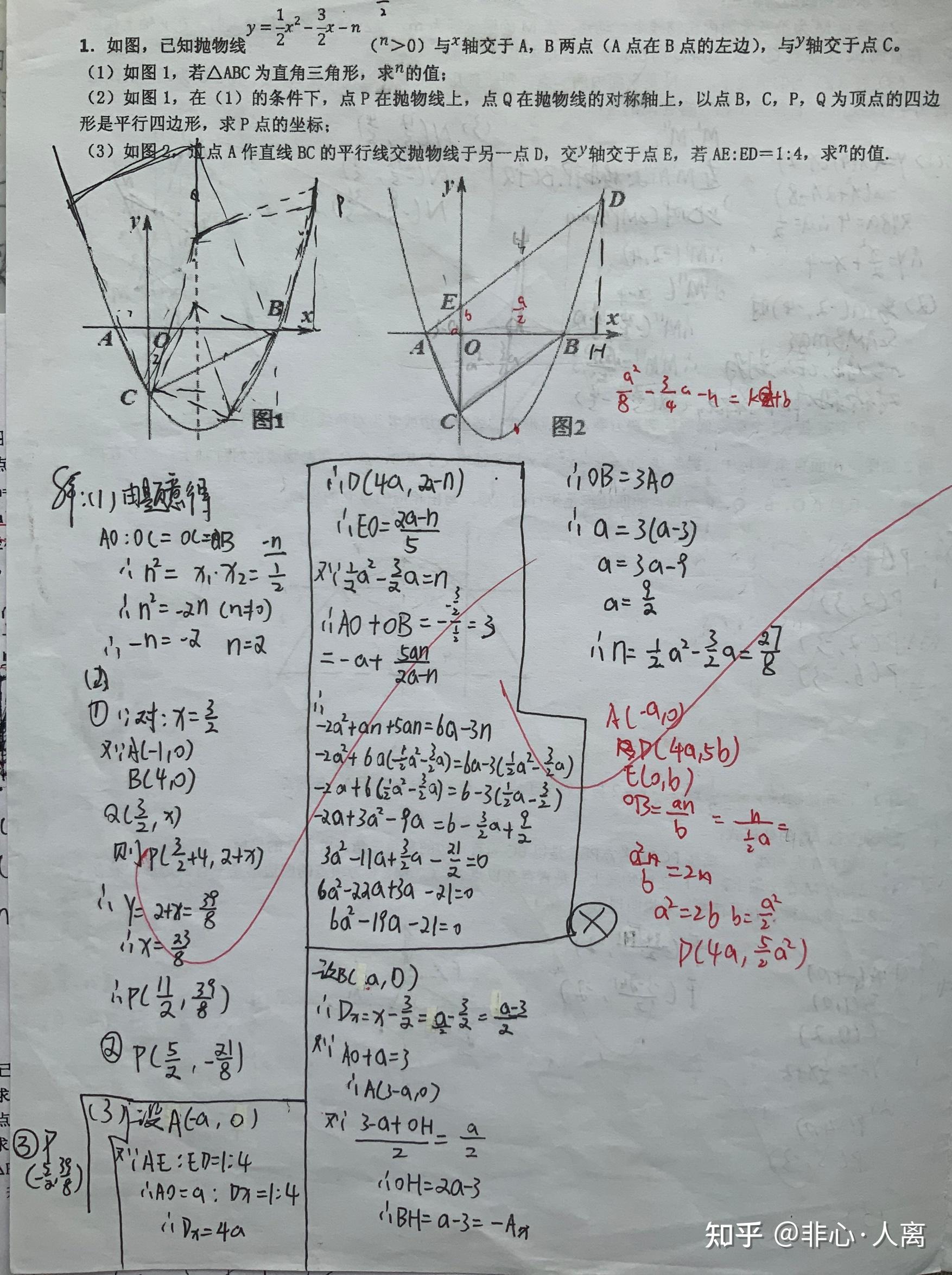
（红笔是记的正常方法）这题最后一问老师们都激烈讨论了一阵子，而我用我自己不正当的导数法很快就做出来了，过程也非常简洁，哈哈反正只看答案。

尽管老师们都不支持我预习大学内容，我也根本没听，但我中考数学还是如愿以偿考了149，算是解气了吧。后来是跟高中同学聊才知道他们竞赛老师早就介绍过了让他们背结论，只是没有记过程罢了，而像那个特殊三角形面积公式和其他题型的做法他们更是当常识一般，只能说怪我没走竞赛，孤陋寡闻了。

害，不过还是好怀念当时学数学的感觉啊，上了高中开始正式预习大学数学才理解了海上钢琴师中的那句台词的含义

“在琴键上，我能用有限的音符创造无限的乐章，

而在这诺大的座城市里，什么都有，却唯独没有尽头”

数学无限的海洋可以用有限的知识去逼近，亦可以用数不清的数学分支去靠近

初中的我仿佛在解决特定问题的琴键上弹出了无数的解决方法，体会到了无数数学思想和快乐。高中的我看到网上的同龄人动不动就泛函分析解析数论抽象代数几何拓扑近世代数范畴论微分流形调和分析，仿佛我就是那个刚刚踏入城市的1900，想学的东西太多而失去了去深究一小部分知识的耐心和勇气，导致什么都学不出自己的发现，也学不出当年那种天人合一的快感了。

现在高三毕业了，自学了一大堆却都没有很深刻的感觉，希望到了大学这样的瓶颈期能早点过吧，就算我们的发现都可能被他人提前知晓了，也希望依然不影响我们感受到幸福，感受到数学这种至高无上的绝对美丽的认知律令吧。

（一些其他想说的

我们应该从小都是在这样一个自己的想法早就被实现过的世界长大的吧

小时候很疑惑为什么相机的画质比肉眼看到的低几个档次，很激动的问父亲可不可以让相机像眼睛一样有两个甚至更多入光口，这样就能有更好的画质了。可爸爸跟我说“早就有了”

小学时看科普书知道了可能存在能赋予粒子质量的希格斯波色子，激动的跟上大学的表哥说后，却被狠狠的嘲笑了，我发誓长大后一定要发现这个粒子，结果没过几年就被科学家发现了

高中在和同学的交流中我发现人对默契有一种抽象的追求，通过很多天的思考后想了一套解释社会现象的理论叫社会契约论，然后有一天无意间看到了一本一模一样叫社会契约论的书，竟然还是古人写的，看了过后发现自己的思想深度连古人都不如

后面打辩论期间在思考亚文化时突然发现人类的基因几千年来基本没有进化，养育后代的成本太小了，并没有大的进化滤网，现代人和社会大多数的问题都是针对远古时期的基因在失去了对应的环境下时的错位

直到我了解到了进化心理学，这些早已经被研究的很深入了

还有一次一个同学问我为什么sin可以被写成无穷级数，我随口答了一句：因为有无穷个零点，事后我突然发现如果把sin写成零点乘积的形式展开后系数明显和原来熟悉的级数是不一样的，从而可以把pai和级数建立等式，兴奋了半天还是因为技术有限推导时卡了，没忍住就上网查了查，结果竟然是欧拉解决巴塞尔问题时的核心思想，顿时感觉错过了一个亿。

而最离谱的一次是在打游戏时，有一个怪物战，碰到一个选怪顺序和我一样的对手，结果出场后呈镜像排列，两边都一动不动，我就这么无语地盯着这个对称的画面，可能是bug，最前面的怪被空气墙平移了一点，结果两边突然就打起来了，看着不断熵增的战斗场面，我有了一种“打破对称导致演化”的想法，好巧不巧，当天晚上公众号就推我了一个“对称破缺”的讲座，看完后人都傻了，“对称破缺”不仅解释了正反物质量不对称和宇宙演化的必然性，还是跨学科临界点及“多者异也”理论的最佳解释，差点没叫出声。。。

其实每个人都有好多好多珍贵的想法和瞬间，但也许抓住并实现他们的能力就是人与人的差距吧，有些东西可能不去查就也不会继续深究了，而真正的学问其实就在其中，在每一个天马行空的想法里，在每一个我们约定俗成的事物里，希望我们在这个“后知识”的时代能重拾深度思考的能力，也许你需要的并没有那么多，那些渴望的无限，会在你用88个有限琴键奏出的无限乐章中，悄然到来吧